Не нашел поста, посвященного сию мероприятию, поэтому начну его здесь.
В отличие от первых двух довольно стандартных задач, третья задача была реально интересной (по крайней мере, для любителей мат.статистики/эконометрики вроде меня). Интересно, как народ ее сдавал?
Я пробовал различные статистики для разделения перестановок, но лучшее что нашел — p[i]^3 * i, она дает точность распознавания примерно 85%, но, к сожалению, в этой задаче этого мало (нужно ~90%).









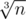 , and, given A, B cannot exceed
, and, given A, B cannot exceed 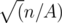 . Then all solution is just two cycles:
. Then all solution is just two cycles: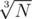 . That's why all similar solutions and maybe some other streetmagic that has anything common with divisors of N, should get AC.
. That's why all similar solutions and maybe some other streetmagic that has anything common with divisors of N, should get AC.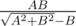 при A <= B;
при A <= B;
