Hello everyone, we are happy to announce that the 2nd Universal Cup has started officially.
The Universal Cup is a non-profit organization dedicated to offering training resources for competitive programming teams. Our website is https://ucup.ac/ (in English and Chinese).
In the previous season, over 750 teams from more than 300 affiliations all over the world, registered and participated in a total of 22 stages, encompassing contests from Asia, Europe, and America.
With the permission of contest setters and without involving copyright disputes, the Universal Cup will hold mirror contests for some undisclosed competition sets. It is expected to hold at least 20 contests in this season. We will simulate the actual situation in the competition, executing the board freeze in the last hour. At the same time, we will provide an overall rating board, which will help the team to make a reasonable assessment of itself.
Over the past few weeks, the committee has worked hard to schedule stages and try to improve the competing experience for participants. We are very excited to share some information here as a head up:
In the upcoming 2nd Universal Cup, starting from September 2nd, 2023, we have already scheduled 14 high-quality stages from Asia and Europe mainly. The current schedule can be viewed on the main page of our website https://ucup.ac/.
There are also 4 stages (expected on October 7th, 14th, 21st, and December 9th) in confirming. The schedule in the second half will also be updated later.
We have managed to upgrade our judging system on QOJ, and we will use it as the contest platform starting this season. To provide more flexibility, instead of 3 fixed time windows, teams now can choose to start to compete in one of the following 6 windows as they want:
- 13:00 (UTC +8) on Saturday ~ 18:00 (UTC +8) on Saturday
- 16:00 (UTC +8) on Saturday ~ 21:00 (UTC +8) on Saturday
- 19:00 (UTC +8) on Saturday ~ 24:00 (UTC +8) on Saturday
- 21:00 (UTC +8) on Saturday ~ 02:00 (UTC +8) on Sunday
- 23:00 (UTC +8) on Saturday ~ 04:00 (UTC +8) on Sunday
- 02:00 (UTC +8) on Sunday ~ 07:00 (UTC +8) on Sunday
For teams that have already registered, if they have done at least 3 contests in the previous season, their account will be preserved and enrolled into the current season automatically. Otherwise, the same as new teams, please register following the instructions on Registration.
The official website has been upgraded. You are able to view all information from the previous by simply choosing the corresponding season on the website.
The first contest will be the stage Qingdao on September 2nd, 2023. The contest source is The 2018 ACM-ICPC Asia Qingdao Regional Online Contest prepared by SUA Problem Setter Team. For a great number of Chinese teams, we believe this will be a good practice to prepare for the upcoming ICPC preliminary online contests in late September.
As well as many other future stages, this stage will be uploaded to Gym afterward. We are grateful to MikeMirzayanov for letting us advertise Universal Cup in Codeforces and providing the great platform Codeforces and Polygon to help prepare contests. We are also very thankful to all contest setters of stages for your support to the Universal Cup. If any setter would like to propose a stage, please feel free to contact us.
Universal Cup Committee:
- Jingbang chenjb Chen
- Yuhao jqdai0815 Du
- Lingyu jiangly Jiang
- Yaowei Sugar_fan Lyu
- Qingyu Qingyu Shi
- Yaohui quailty Zeng
(Sorted by lexicographical order of the last name)









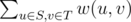 .
. solution.
solution.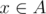 , it's obvious that
, it's obvious that 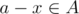 . The contraposition of it is
. The contraposition of it is 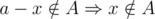 , that means if
, that means if 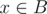 ,
, 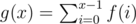 .
. 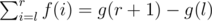 , so we should find a pair of number
, so we should find a pair of number 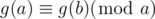
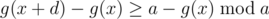 .
.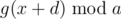 is very small, between
is very small, between 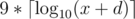 . If
. If 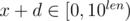 , after choosing
, after choosing 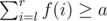 until we find
until we find 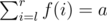 .
.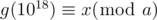 ,
, 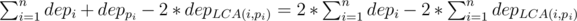
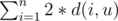 .
.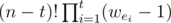 to the answer.
to the answer.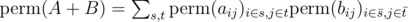 ,
,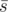 ,
,  are their respective complements in that set.
are their respective complements in that set.
