615A - Лампочки (Автор: TheWishmaster)

Заведем для каждой лампочки счетчик – сколько кнопок ее выключает. Если для какой-то лампочки счетчик равен 0, то ответ нет, иначе да.

Код: 15260902

615B - Длиннохвостый еж (Автор: TheWishmaster)

Посчитаем dp[i] – максимальная длина хвоста, заканчивающегося в i-ой вершине. Обновлять его просто – пройдем по всем ребрам из вершины и попытаемся увеличить текущее значение в концах ребер. Для ответа пройдемся по всем вершинам и выберем лучшую.

Код: 15260851

615C - Беговой трек (Автор: maxkvant)

Заметим, что если мы можем мы можем получить подстроку t[i, j] используя k полотен, то мы можем получить и подстроку t[i + 1, j] не более чем из k полотен. Поэтому нам выгодно каждый раз брать как можно более длинную подстроку.

Пусть n = |s|, m = |t|. На каждом этапе будем за 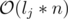искать эту самую длинную подстроку (l_j – ее длина) в s и s_reversed, которую можем приписать к ответу.

Это можно делать несколькими способами:

• Посчитаем lcp[i][j] — наибольший общий префикс t[i, m] и s[j, n], lcprev[i][j] — t[i, m] и s[j, 1]. Найти нужную подстроку означает найти max(max(lcp[i][1], lcp[i][2], ..., lcp[i][n]), max(lcprev[i][1], lcprev[i][2], ..., lcprev[i][n])).

Подсчёт lcp:

for (int i = m; i >= 1; i--)
     for (int j = n; j >= 1; j--) 
          if (t[i] == s[j])
              lcp[i][j] = lcp[i + 1][j + 1] + 1;

Код: 15277213

• Заведём массив endPos, где значит endPos[j] — равна ли t[i, i + cur_len - 1] и s[j - cur_len + 1, j]. Будем пересчитывать значения этого массива, добавляя по одному символу t[i],  t[i + 1],  t[i + 2].... Аналогичный массив заведём для s_reversed. Суммарно решение отработает за

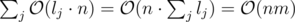
Код: 15260867

Решение бором: 15260870

bonus

можете ли вы решить задачу за , ? ?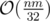

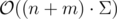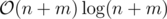Σ — размер алфавита.

615D - Множители (Автор: maxkvant)

Обозначим d(x) — к-во делителей числа x, f(x) — произведение делителей числа. Пусть x = p₁^α₁p₂^α₂... p_n^α_n, тогда d(x) = (α₁ + 1)·(α₂ + 1)... (α_n + 1)

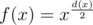. Есть 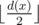пар делителитей вида 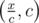, , 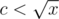и если x — точный квадрат добавляется ещё 1 делитель : .

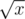для простого m и a ≠ 0 верно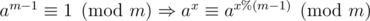

Можно заметь, если a и b взаимно простые, то ,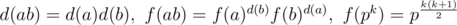

Пользуясь этими свойствами нетрудно посчитать ответ:

d = 1;
ans = 1;
for (int i = 0; i < l; i++) {
    fp = binPow(p[i], (cnt[i] + 1) * cnt[i] / 2);
    ans = binPow(ans, (cnt[i] + 1)) * binPow(fp, d) % MOD;
    d = d * (cnt[i] + 1) % (MOD - 1);
}  

Код: 15260890

bonus

Другая задача.

Дана последовательность (p₁, k₁),  (p₂, k₂), ...,  (p_n, k_n)
(p_i — различные простые) и q запоросов (l, r) вычислить f(p_l^k_l·p_l + 1^k_l + 1... p_r^k_r)%MOD.

Как решать за ?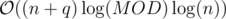

615E - Шестиугольники (Автор: TheWishmaster)

Посмотрим, как изменяется координаты при переходе из текущего 6-угольника в каждый из смежных ему(назовем это 6 типами переходов). Если мы знаем сколько переходов каждого типа мы сделали на пути, то знаем и координаты конца пути.

Разделим весь путь на кольца:

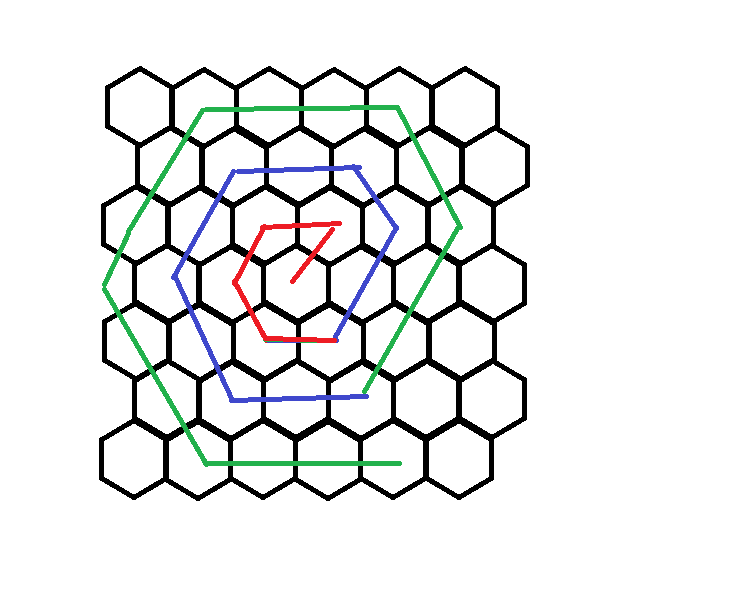
Посчитаем количество переходов через каждую из сторон шестиугольника для 1 кольца. В каждом следующем кольце будет на 1 переход каждого типа больше, чем в предыдущем кольце. Длина каждого кольца = длина предыдущего + 6. Это арифметическая прогрессия. С помощью формулы суммы первых членов арифметической прогрессии и бинпоиска найдем номер последнего кольца и длину всех колец до него. Осталось только перебрать 6 типов последнего сделанного перехода и посчитать ответ.

Код: 15260879