Is there an editorial published somewhere? I have checked UTPC's official website but couldn't find anything. Would love to see some explanations for the harder problems. Participants' solutions can't be viewed, is this intentional too?
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3856 |
| 2 | jiangly | 3747 |
| 3 | orzdevinwang | 3706 |
| 4 | jqdai0815 | 3682 |
| 5 | ksun48 | 3591 |
| 6 | gamegame | 3477 |
| 7 | Benq | 3468 |
| 8 | Radewoosh | 3462 |
| 9 | ecnerwala | 3451 |
| 10 | heuristica | 3431 |
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 167 |
| 2 | -is-this-fft- | 162 |
| 3 | Dominater069 | 160 |
| 4 | Um_nik | 158 |
| 5 | atcoder_official | 157 |
| 6 | Qingyu | 156 |
| 7 | adamant | 151 |
| 7 | djm03178 | 151 |
| 7 | luogu_official | 151 |
| 10 | awoo | 146 |
Recently, I have been reading up on few blogs about rolling hash: dacin21's [On the mathematics behind rolling hashes and anti-hash tests] and rng_58's [Hashing and Probability of Collision]. Both of them showcase different hashing technique.
Method described in dacin21's blog:
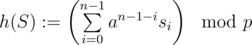
Note: in the above equation a is the base
Method described in rng_58's blog:
H(a) = (r+a_1)(r+a_2)...(r+a_n)
Note: in the above equation r is the base
Are there any differences between the two in terms of use-case and other parameters? Which one do you recommend? Also, if possible can you please share your implementation of rolling hash if you have ever used it to solve any problem. Thanks!
Can't understand how to solve this problem.
Find a permutation of a given sequence A with N elements, such that it is a max-heap and when converting it to a sorted sequence, the total number of swaps in maxHeapify of line 25 in the pseudo code is maximal possible.
1 maxHeapify(A, i)
2 l = left(i)
3 r = right(i)
4 // select the node which has the maximum value
5 if l ≤ heapSize and A[l] > A[i]
6 largest = l
7 else
8 largest = i
9 if r ≤ heapSize and A[r] > A[largest]
10 largest = r
11
12 if largest ≠ i
13 swap A[i] and A[largest]
14 maxHeapify(A, largest)
15
16 heapSort(A):
17 // buildMaxHeap
18 for i = N/2 downto 1:
19 maxHeapify(A, i)
20 // sort
21 heapSize ← N
22 while heapSize ≥ 2:
23 swap(A[1], A[heapSize])
24 heapSize--
25 maxHeapify(A, 1)
Source: AOJ
| Name |
|---|










