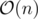631A - Собеседование

Для решения задачи достаточно знать один факт: 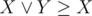. Его достаточно просто доказать, воспользовавшись таблицей истинности. Пользуясь этим фактом получаем: 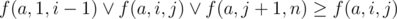и 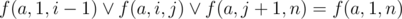. На основании двух предыдущих формул получим: f(a, 1, n) ≥ f(a, i, j). Несложно догадаться, что ответ будет равен f(a, 1, n) + f(b, 1, n).

Время: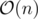

Память: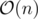

C++ Python3

631B - Проверка печати

Пусть timeR_i — номер последнего запроса, который перекрашивает строку i, а timeC_j — номер последнего запроса, который перекрашивает столбец j. Очевидно, что значение таблицы в ячейке (i, j) будет равно a_{max(timeRi, timeCj)}.

Время: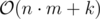

Память: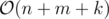

C++ Python3

631C - Отчёт

Если существует пара запросов r_i ≥ r_j, i > j, то мы сможем опустить запрос j. После того, как мы опустим подобные запросы, то мы получим отсортированный массив запросов (r_i ≤ r_j, i > j). Давайте отсортируем a_1..max(ri) и скопируем его в b. Несложно догадаться что для обработки запроса i достаточно записать в подмассив a_{ri + 1..ri} первые или последние

Unable to parse markup [type=CF_TEX]

элементов b. После этого надо извлечь эти элементы из b. Проделаем эту операцию по всем i (1 ≤ i < n), не забывая что после выполнения запросов надо отсортировать a_1..rn.

Время: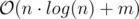

Память: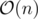

C++ Python3

631D - Мессенджер

Пусть S[i] — это блок S с номером i, T[i] — это блок T с номером i. При этом

Unable to parse markup [type=CF_TEX]

и T[l..r] = T[l]T[l + 1]...T[r].

T является подстрокой S, если S[l + 1..r - 1] = T[2..m - 1] и S[l].l = T[1].l и S[l].c ≥ T[1].c и S[r].l = T[m].l и S[r].c ≥ T[m].c. Найдём все вхождения T[l + 1..r - 1] в S и выберем только те, из которых можно получить T. Это можно сделать с помощью алгоритма Кнута-Морриса-Пратта.

В задаче есть несколько крайних случаев:

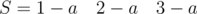1. и 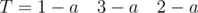. Одинаковые буквы в соседних блоках. С этой проблемой можно бороться объединением соседних блоков.

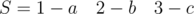2. и 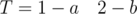. Количество блоков T меньше трёх. Подобные тесты следует обрабатывать отдельно.

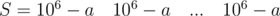3. и 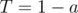. Ответ для таких тестов не влазит в 32-битный тип.

Время: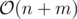

Память: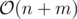

C++Python3

631E - Мультипликативная сумма

Решение за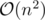

Заметим, что операция, описанная в условии, является операцией циклического сдвига некоторого подмассива. Рассмотрим решение для циклического сдвига вправо и влево по отдельности. Но cначала введём некоторые обозначения: 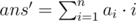— ответ до циклического сдвига, Δans — изменение ответа после циклического сдвига. Ответом на задачу будет ans = ans' + Δans. Δans будем искать перебирая все циклические сдвиги (l, r).

Распишем формулу для левого сдвига:

Δ_l, r = (a_l·r + a_l + 1·l + ... + a_r·(r - 1)) - (a_l·l + a_l + 1·(l + 1) + ... + a_r·r) = a_l·(r - l) - (a_l + 1 + a_l + 2 + ... + a_r)

Теперь для правого сдвига:

Δ'_l, r = (a_l·(l + 1) + a_l + 1·(l + 2) + ... + a_r·l) + (a_l·l + a_l + 1·(l + 1) + ... + a_r·r) = (a_l + a_l + 1 + ... + a_r - 1) + a_r·(l - r)

Если применить префикс суммы sum_r — сумма на префиксе [1, r], то можно находить эти значения за .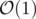

Полное решение за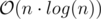

Перепишем формулы для сдвигов:

Для левого сдвига: Δ_l, r = (a_l·r - sum_r) + (sum_l - a_l·l)

Для правого сдвига: Δ'_l, r = (a_r·l - sum_l - 1) + (sum_r - 1 - a_r·r)

Если для левого сдвига фиксировать l, а для правого сдвига фиксировать r, то можно применить Convex Hull Trick.

Время: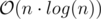

Память:

C++