DIV2A-DZY Loves Chessboard
Just output the chessboard like this:
WBWBWBWB...
BWBWBWBW...
WBWBWBWB...
...
Don't forget to left '-' as it is. The time complexity is O(nm).
check the C++ code here.
DIV2B-DZY Loves Chemistry
It's easy to find that answer is equal to 2n - v, where v is the number of connected components.
check the C++ code here.
DIV1A-DZY Loves Physics
If there is a connected induced subgraph containing more than 2 nodes with the maximum density. The density of every connected induced subgraph of it that contains only one edge can be represented as 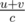 , where u, v are the values of the two nodes linked by the edge. The density of the bigger connected induced subgraph is at most
, where u, v are the values of the two nodes linked by the edge. The density of the bigger connected induced subgraph is at most 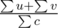 .
.
If 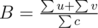 , and for every edge,
, and for every edge, 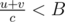 . Then we'll have u + v < Bc, and
. Then we'll have u + v < Bc, and 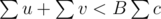 , and
, and 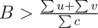 , it leads to contradiction.
, it leads to contradiction.
So just check every single node, and every 2 nodes linked by an edge.
The time complexity is O(n + m).
check the C++ code here.
DIV1B-DZY Loves FFT
Firstly, you should notice that A, B are given randomly.
Then there're many ways to solve this problem, I just introduce one of them.
This algorithm can get Ci one by one. Firstly, choose an s. Then check if Ci equals to n, n - 1, n - 2... n - s + 1. If none of is the answer, just calculate Ci by brute force.
The excepted time complexity to calculate Ci - 1 is around
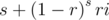
where 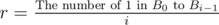 .
.
Just choose an s to make the formula as small as possible. The worst excepted number of operations is around tens of million.
check the C++ code here.
DIV1C-DZY Loves Colors
The only thing you need to notice is that if there are many continuous units with the same uppermost color, just merge them in one big unit. Every time painting continuous units, such big units will only increase by at most 3. Then you can use STL set to solve it. But anyway, a segment tree is useful enough, check the C++ solution here.
The time complexity is  .
.
DIV1D-DZY Loves Strings
We can solve a subproblem in which all the query strings are characters only first. The problem becomes calculating the shortest substring containing two given characters.
If character ch appears more than T times in S, use brute force with time complexity O(|S|) to calculate all the queries containing ch. Obviously, there are at most O(|S| / T) such ch in S.
Otherwise, we consider two sorted sequences, just merge them with time complexity O(T)(Both of the two characters appear at most T times). Being merging, you can get the answer.
So the complexity is O(TQ + |S|2 / T). We can choose 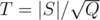 , then the complexity is
, then the complexity is 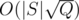 .
.
And short substring is almost the same with characters.
Check the C++ code here.
DIV1E-DZY Loves Planting
Firstly, use binary search. We need to determine whether the answer can be bigger than L. Then, every pair (i, Pi) must contain at least one edge which length is bigger than L. It's a problem like bipartite graph matching, and we can use maxflow algorithm to solve it.
We create 2 nodes for every node i of the original tree. We call one of the nodes Li, and the other Ri. And we need a source s and a terminal t. Link s to every Li with upper bound 1, and link Ri to t with upper bound xi. Then if the path between node a and node b contains an edge with value larger than L, link La and Rb with upper bound 1. This means they can match. Every time we build such graph, we must check O(N2) pairs of nodes, so number of edges of the network is O(N2).
We can make it better. Consider the process of \texttt{Divide and Conquer} of a tree, This algorithm can either based on node or edge. And The one based on edge is simpler in this problem. Now, there are two subtrees Tx, Ty on two sides, we record the maximum edge from every node i to the current edge we split, we call it MAXLi.
Suppose Lx is in Tx and Ry is in Ty (it is almost the same in contrast). We create two new nodes Gx, Gy in the network to represent the two subtrees. Add edges (Li, Gx, ∞) (i is in Tx) and edges (Gy, Ri, ∞) (i is in Ty). If i is in Tx and MAXLi > L, we add an edge (Li, Gy, ∞). If j is in Ty and MAXLj > L, we add an edge (Gx, Rj, ∞).
Then use maxflow algorithm. The number of nodes in the network is O(N) and the number of edges in the network is 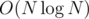 . So the total complexity is
. So the total complexity is 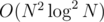 with really small constant.
with really small constant.
Check the C++ code here.
This is what I supposed DIV1-E will be. And thank subscriber for coming up with a really good algorithm with time complexity O(nα(n)) 7025382. And maybe others have the same idea. This is my mistake, and I feel sorry for not noticing that, I'm too naive, and not good at solving problems. Please forgive me.









