| Codeforces Round 497 (Div. 1) |
|---|
| Закончено |
В упрощённой версии игры мини-метро есть только одна линия метро, на которой поезда ходят всегда в одну сторону. На линии расположено $$$n$$$ станций, на $$$i$$$-й станции в начале игры ждут поезда $$$a_i$$$ людей. Игра начинается в начале $$$0$$$-го часа. В конце каждого часа (за пару минут до конца часа) на станцию $$$i$$$ мгновенно прибывают ещё $$$b_i$$$ людей. Если в какой-то момент число людей на $$$i$$$-й станции превышает $$$c_i$$$, то вы проиграли.
У игрока в распоряжении есть несколько поездов, которые он может распределить по часам. Вместимость каждого поезда — $$$k$$$ пассажиров. В середине назначенного ему часа поезд моментально проходит с $$$1$$$-й по $$$n$$$-ю станции, забирая с каждой станции столько человек, сколько ещё может вместить. То есть поезд не может забрать людей со станции $$$i$$$, если ещё есть люди на станции $$$i-1$$$.
Если несколько поездов распределены в один час, их вместимости складываются, и они движутся вместе.
Игрок хочет продержаться в игре $$$t$$$ часов. Определите, какое минимальное число поездов ему для этого потребуется.
Первая строка содержит три целых числа $$$n$$$, $$$t$$$ и $$$k$$$ ($$$1 \leq n, t \leq 200, 1 \leq k \leq 10^9$$$) — количество станций на линии, количество часов, которое мы хотим продержаться, и вместимость каждого поезда, соответственно.
Каждая из следующих $$$n$$$ строк содержит три целых числа $$$a_i$$$, $$$b_i$$$ и $$$c_i$$$ ($$$0 \leq a_i, b_i \leq c_i \leq 10^9$$$) — количество людей на $$$i$$$-й станции в начале игры, количество людей, прибывающих на $$$i$$$-ю станцию в конце каждого часа, и максимальное разрешенное число людей на $$$i$$$-й станции, соответственно.
Выведите одно целое число — ответ на задачу.
3 3 10
2 4 10
3 3 9
4 2 8
2
4 10 5
1 1 1
1 0 1
0 5 8
2 7 100
12
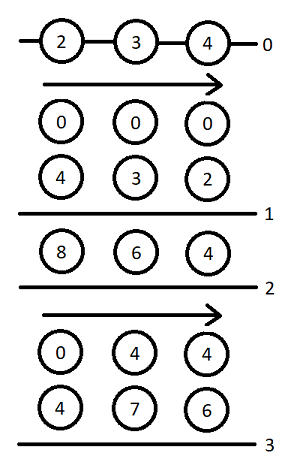
Рассмотрим тест из условия. Есть три станции, на первой изначально 2 человека, на второй — 3, а на третьей — 4. Максимальная вместимость станций — 10, 9 и 8 соответственно.
Одна из выигрышных стратегий — это пустить два поезда в первый и третий часы. Тогда в первый час поезд забирает всех людей со всех станций, а затем, в конце часа на первую станцию прибывают 4 человека, на вторую — 3, а на третью — 2.
Во второй час поезд не приходит, и в конце на станции вновь прибывают столько же человек.
В третий час поезд сначала забирает 8 человек с первой станции и, прибыв на вторую, забирает лишь 2 человека, потому что может вместить не более 10. Затем, он проезжает мимо третьей станции, поскольку поезд и так уже полон. После этого на станции вновь прибывают люди, и игра заканчивается.
Так как ни в какой момент на станции не было больше человек, чем она может вместить, то мы выиграли, использовав два поезда.
| Название |
|---|




