Назовем неориентированный граф $$$G = (V, E)$$$ взаимно простым, если для каждого ребра $$$(v, u) \in E$$$ $$$GCD(v, u) = 1$$$ (наибольший общий делитель $$$v$$$ и $$$u$$$ равен $$$1$$$). Если между некоторой парой вершин $$$v$$$ и $$$u$$$ нет ребра, то значение $$$GCD(v, u)$$$ не важно. Вершины нумеруются от $$$1$$$ до $$$|V|$$$.
Постройте взаимно простой граф из $$$n$$$ вершин и $$$m$$$ ребер такой, что он связный, не содержит петель и кратных ребер.
Если не существует корректного графа с данным числом вершин и ребер, то выведите «Impossible».
Если существует несколько ответов, то выведите любой из них.
В единственной строке записаны два целых числа $$$n$$$ и $$$m$$$ ($$$1 \le n, m \le 10^5$$$) — количество вершин и количество ребер в графе.
Если не существует корректного графа с данным числом вершин и ребер, то выведите «Impossible».
В противном случае выведите ответ в следующем формате:
В первой строке должно быть записано слово «Possible».
В $$$i$$$-й из следующих $$$m$$$ строк должно содержаться $$$i$$$-е ребро $$$(v_i, u_i)$$$ полученного графа ($$$1 \le v_i, u_i \le n, v_i \neq u_i$$$). Для каждой пары $$$(v, u)$$$ не должно больше содержаться пар $$$(v, u)$$$ или $$$(u, v)$$$. Вершины нумеруются от $$$1$$$ до $$$n$$$.
Если существует несколько ответов, то выведите любой из них.
5 6
Possible
2 5
3 2
5 1
3 4
4 1
5 4
6 12
Impossible
Изображение графа из первого примера: 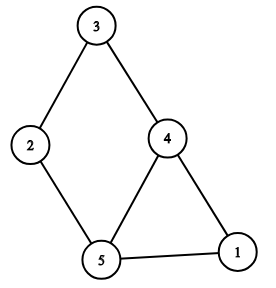
| Название |
|---|




