Задан набор из $$$2n+1$$$ целочисленных точек на декартовой плоскости. Точки пронумерованы от $$$0$$$ до $$$2n$$$ включительно. Пусть $$$P_i$$$ — $$$i$$$-я точка. Тогда $$$x$$$-координата точки $$$P_i$$$ равна $$$i$$$. $$$y$$$-координата точки $$$P_i$$$ равна нулю (изначально). Таким образом, изначально $$$P_i=(i,0)$$$.
Заданный набор точек является вершинами графика кусочной функции. $$$j$$$-й кусок функции — отрезок $$$P_{j}P_{j + 1}$$$. За один ход вы можете увеличить на $$$1$$$ $$$y$$$-координату любой точки с нечетной $$$x$$$-координатой (то есть точек $$$P_1, P_3, \dots, P_{2n-1}$$$). Заметьте, что соответствующие отрезки тоже меняются.
Например, график ниже иллюстрирует функцию для $$$n=3$$$ (количество точек равно $$$2\cdot3+1=7$$$), в которой мы увеличили $$$y$$$-координату точки $$$P_1$$$ три раза и $$$y$$$-координату точки $$$P_5$$$ один раз:
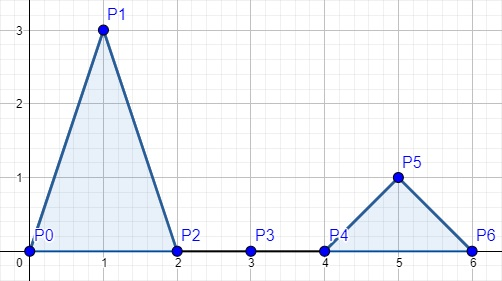
Пусть площадь графика равна площади под графиком, но над координатной прямой OX. Тогда площадь графика на картинке выше равна 4 (голубая площадь на картинке выше — это площадь графика, нарисованного на ней).
Пусть высота графика равна максимальной $$$y$$$-координате среди всех изначальных точек графика (то есть точек $$$P_0, P_1, \dots, P_{2n}$$$). Высота графика на картинке выше равна 3.
Ваша задача — найти, какую минимальную высоту может иметь график, состоящий из $$$2n+1$$$ вершин с площадью, равной $$$k$$$. Заметьте, что необязательно минимизировать количество ходов.
Легко заметить, что любой ответ, который может быть получен при помощи применения описанных выше ходов, всегда существует и является целым числом, не превосходящим $$$10^{18}$$$.
Первая строка входных данных содержит два целых числа $$$n$$$ и $$$k$$$ ($$$1 \le n, k \le 10^{18}$$$) — количество вершин в графике кусочной функции и площадь, которую мы должны получить.
Выведите одно целое число — минимально возможную высоту графика, состоящего из $$$2n+1$$$ вершин с площадью, равной $$$k$$$. Легко заметить, что любой ответ, который может быть получен при помощи применения описанных выше ходов, всегда существует и является целым числом, не превосходящим $$$10^{18}$$$.
4 3
1
4 12
3
999999999999999999 999999999999999986
1
Один из возможных ответов на первый тестовый пример:
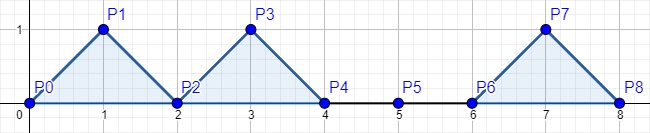
Площадь этого графика равна 3, высота этого графика равна 1.
Единственный возможный ответ на второй тестовый пример:
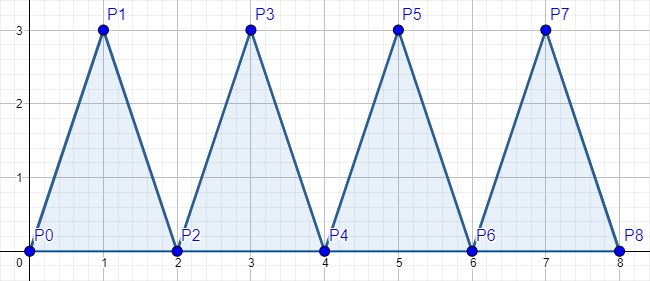
Площадь этого графика равна 12, высота этого графика равна 3.
| Название |
|---|




