Задано $$$n$$$ отрезков на декартовой плоскости. Концы каждого отрезка имеют целочисленные координаты. Отрезки могут пересекаться друг с другом. Никакие два отрезка не лежат на одной прямой.
Посчитайте количество различный точек с целочисленными координатами, которые покрыты хотя бы одним отрезком.
В первой строке записано одно целое число $$$n$$$ ($$$1 \le n \le 1000$$$) — количество отрезков.
В каждой из следующих $$$n$$$ строк записаны по четыре целых числа $$$Ax_i, Ay_i, Bx_i, By_i$$$ ($$$-10^6 \le Ax_i, Ay_i, Bx_i, By_i \le 10^6$$$) — координаты концов $$$A$$$, $$$B$$$ ($$$A \ne B$$$) $$$i$$$-го отрезка.
Гарантируется, что никакие два отрезка не лежат на одной прямой.
Выведите единственное число — количество различных точек с целочисленными координатами, которые покрыты хотя бы одним отрезком.
9
0 0 4 4
-1 5 4 0
4 0 4 4
5 2 11 2
6 1 6 7
5 6 11 6
10 1 10 7
7 0 9 8
10 -1 11 -1
42
4
-1 2 1 2
-1 0 1 0
-1 0 0 3
0 3 1 0
7
Картинка для первого примера:
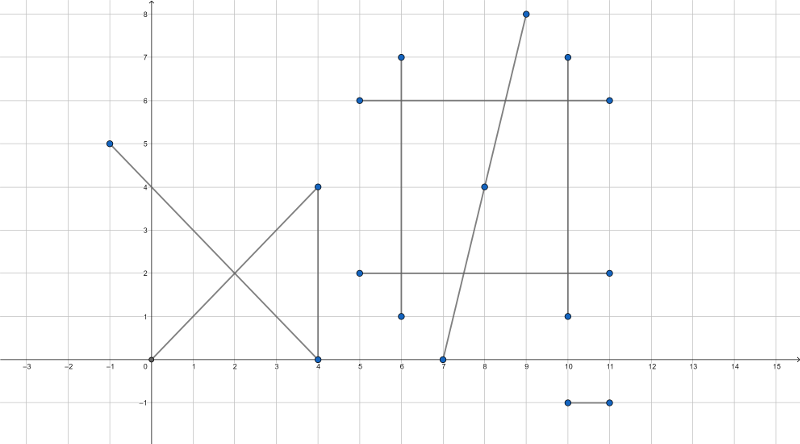
Некоторые ключевые точки отмечены синим, в ответе также содержатся и некоторые непомеченные точки.
Картинка для второго примера:

| Название |
|---|




