| Codeforces Round 509 (Div. 2) |
|---|
| Закончено |
Самолет летит параллельно поверхности земли на высоте $$$h$$$ метров. Будем считать, что самолет летит из точки $$$(-10^9, h)$$$ в точку $$$(10^9, h)$$$ параллельно оси $$$Ox$$$ вправо.
В самолете находится планерист, который в определенный момент выпрыгнет из самолета. Из-за особенностей задачи, планерист может выпрыгивать только в целочисленных координатах. После прыжка каждую секунду он будет двигаться вдоль оси $$$Ox$$$ на единицу вправо, а также падать на единицу вниз.
На некоторых отрезках действуют восходящие потоки воздуха, характеризующиеся двумя числами $$$x_1$$$ и $$$x_2$$$ ($$$x_1 < x_2$$$). Они действуют по всей высоте. Никакие два потока не пересекаются и не имеют общих точек. Если планерист попадает в восходящий поток, то он не теряет высоту, пока летит в этом потоке. Изменение по оси $$$Ox$$$ остается таким же — он двигается на единицу вправо за одну секунду.
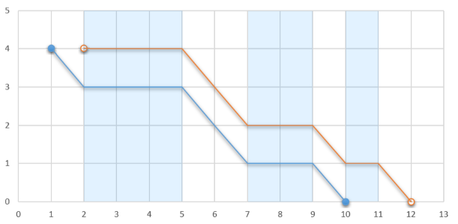Если планерист выпрыгнет в координате $$$1$$$, то он остановится в $$$10$$$. Если же он выпрыгнет в $$$2$$$, то остановится в $$$12$$$. Определите максимальное расстояние по оси $$$Ox$$$ от точки прыжка до точки приземления, которое планерист сможет пролететь, если он самостоятельно может выбрать точку прыжка. Коснувшись земли, планерист останавливается, то есть он не может планировать в восходящем потоке на высоте $$$0$$$.
Первая строка содержит два целых числа $$$n$$$ и $$$h$$$ $$$(1 \le n \le 2\cdot10^{5}, 1 \le h \le 10^{9})$$$ — количество восходящих потоков воздуха и высота полета самолета.
Каждая из следующих $$$n$$$ строк содержит два целых числа $$$x_{i1}$$$ и $$$x_{i2}$$$ $$$(1 \le x_{i1} < x_{i2} \le 10^{9})$$$ — координаты левого и правого концов $$$i$$$-го восходящего потока. Гарантируется, что никакие два потока не пересекаются и не имеют общих точек. Потоки заданы в порядке возрастания их координат.
Выведите максимальное расстояние по оси $$$Ox$$$ от точки прыжка до точки приземления, которое планерист сможет пролететь, если он самостоятельно может выбрать точку прыжка. Гарантируется, что при заданных ограничениях ответ целочисленный.
3 4
2 5
7 9
10 11
10
5 10
5 7
11 12
16 20
25 26
30 33
18
1 1000000000
1 1000000000
1999999999
В первом примере планеристу выгодно выпрыгнуть в точке с координатами $$$(2, 4)$$$, тогда он приземлится в точке $$$(12, 0)$$$, что даст расстояние равное $$$12-2 = 10$$$.
Во втором примере планеристу выгодно выпрыгнуть в точке с координатами $$$(16,10)$$$, тогда он приземлится в точке $$$(34,0)$$$, что даст расстояние равное $$$34-16=18$$$.
В третьем примере планерист может выпрыгнуть, например, в точке с координатами $$$(-100,1000000000)$$$, тогда он приземлится в точке $$$(1999999899,0)$$$, что даст расстояние равное $$$1999999899-(-100)=1999999999$$$.
