| Codeforces Round 510 (Div. 2) |
|---|
| Закончено |
Вам дано неориентированное дерево, состоящее из $$$n$$$ вершин.
Назовём вершину листом, если она соединена ровно с одной другой вершиной.
Под расстоянием между двумя вершинами будем понимать количество рёбер на кратчайшем пути между этими вершинами.
Назовем некоторое множество листьев красивым, если максимальное расстояние между любой парой листьев из этого множества не превышает $$$k$$$.
Перед вами стоит задача разделить все листья дерева на непересекающиеся красивые множества. Определите минимальное количество множеств, которые можно получить в результате описанного разделения.
В первой строке следуют два целых числа $$$n$$$ и $$$k$$$ ($$$3 \le n \le 10^6$$$, $$$1 \le k \le 10^6$$$) — количество вершин в дереве и максимальное расстояние между парой листьев, принадлежащих одному красивому множеству.
Каждая из следующих $$$n - 1$$$ строк содержит по два целых числа $$$v_i$$$ и $$$u_i$$$ ($$$1 \le v_i, u_i \le n$$$) — описание $$$i$$$-го ребра дерева.
Гарантируется, что описанные рёбра формируют дерево.
Выведите минимальное количество красивых множеств в разбиении всех листьев.
9 3
1 2
1 3
2 4
2 5
3 6
6 7
6 8
3 9
2
5 3
1 2
2 3
3 4
4 5
2
6 1
1 2
1 3
1 4
1 5
1 6
5
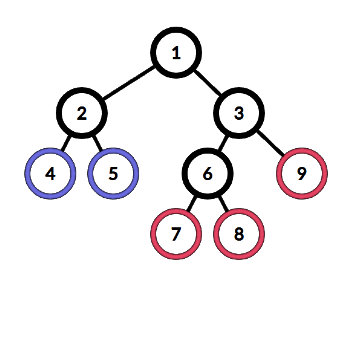
Картинка описывает разбиение дерева из первого примера.
| Название |
|---|




