Даны два массива $$$a$$$ и $$$b$$$ из целых положительных чисел, длины $$$n$$$ и $$$m$$$ соответственно.
Рассмотрим матрицу $$$c$$$ размера $$$n \times m$$$, где $$$c_{i,j} = a_i \cdot b_j$$$.
Вам необходимо найти в матрице $$$c$$$ подпрямоугольник максимальной площади, сумма чисел в котором не превосходит $$$x$$$.
Формально, необходимо найти такую максимальную площадь $$$s$$$, что существуют четыре целых числа $$$x_1, x_2, y_1, y_2$$$, удовлетворяющих ограничениям $$$1 \leq x_1 \leq x_2 \leq n$$$, $$$1 \leq y_1 \leq y_2 \leq m$$$, $$$(x_2 - x_1 + 1) \times (y_2 - y_1 + 1) = s$$$, таких что $$$$$$\sum_{i=x_1}^{x_2}{\sum_{j=y_1}^{y_2}{c_{i,j}}} \leq x.$$$$$$
В первой строке записаны два целых числа $$$n$$$ и $$$m$$$ ($$$1 \leq n, m \leq 2000$$$).
Во второй строке записаны $$$n$$$ целых чисел $$$a_1, a_2, \ldots, a_n$$$ ($$$1 \leq a_i \leq 2000$$$).
В третьей строке записаны $$$m$$$ целых чисел $$$b_1, b_2, \ldots, b_m$$$ ($$$1 \leq b_i \leq 2000$$$).
В четвертой строке записано одно целое число $$$x$$$ ($$$1 \leq x \leq 2 \cdot 10^{9}$$$).
Если существуют четыре целых числа $$$x_1, x_2, y_1, y_2$$$, таких что $$$1 \leq x_1 \leq x_2 \leq n$$$, $$$1 \leq y_1 \leq y_2 \leq m$$$ и $$$\sum_{i=x_1}^{x_2}{\sum_{j=y_1}^{y_2}{c_{i,j}}} \leq x$$$, выведите максимально возможное значение $$$(x_2 - x_1 + 1) \times (y_2 - y_1 + 1)$$$ среди всех подходящих четвёрок, иначе выведите $$$0$$$.
3 3
1 2 3
1 2 3
9
4
5 1
5 4 2 4 5
2
5
1
Матрица из первого примера и выбранный подпрямоугольник (синего цвета):
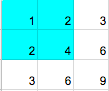
Матрица из второго примера и выбранный подпрямоугольник (синего цвета):

| Название |
|---|




