У Вас есть игрушечное здание состоящее из $$$n$$$ башен. Каждая башня является столбиком кубиков, стоящих друг на друге. $$$i$$$-я башня состоит из $$$h_i$$$ кубиков и, соответственно, имеет высоту $$$h_i$$$.
Объявим операцию срезания по некоторой высоте $$$H$$$ следующим образом: для каждой башни $$$i$$$, если её текущая высота больше $$$H$$$, то уберем несколько верхних кубиков так, чтобы высота башни стала равна $$$H$$$. Стоимость одного «срезания» равна суммарному количеству убранных кубиков со всех башен.
Назовем срез хорошим, если его стоимость меньше или равна $$$k$$$ ($$$k \ge n$$$).
Определите минимально возможное количество хороших срезов, необходимых для того, чтобы сделать все башни равными по высоте. Очевидно, что всегда существует способ выровнять башни.
Первая строка содержит два целых числа $$$n$$$ и $$$k$$$ ($$$1 \le n \le 2 \cdot 10^5$$$, $$$n \le k \le 10^9$$$) — количество башен и ограничение на срезы.
Вторая строка содержит $$$n$$$ целых чисел $$$h_1, h_2, \dots, h_n$$$ ($$$1 \le h_i \le 2 \cdot 10^5$$$) — первоначальные высоты башен.
Выведите единственное число — минимально возможное количество хороших срезов, необходимых для того, чтобы сделать все башни равными по высоте.
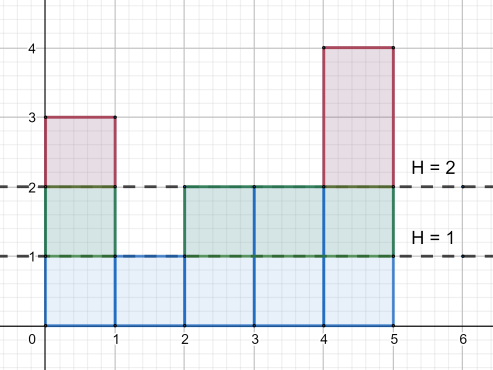
5 5
3 1 2 2 4
2
4 5
2 3 4 5
2
В первом примере выгодно сделать $$$2$$$ операции срезания. Первый срез по высоте $$$2$$$ (его стоимость равна $$$3$$$) и второй по высоте $$$1$$$ (его стоимость равна $$$4$$$).
| Название |
|---|




