Вам задано дерево из $$$n$$$ вершин с корнем в вершине $$$1$$$. Также на данном дереве расположена фишка. Первоначально фишка находится в корне дерева. Вы можете двигать фишку по ребрам дерева следующим образом: пусть текущая вершина с фишкой $$$v$$$, тогда у вас есть два возможных хода:
- спуститься к любому листу поддерева вершины $$$v$$$;
- если вершина $$$v$$$ — лист, то подняться вверх по дереву не более чем $$$k$$$ раз. Другими словами, если $$$h(v)$$$ — глубина вершины $$$v$$$ (глубина корня равна $$$0$$$), то вы можете передвинуть фишку в вершину $$$to$$$ такую, что $$$to$$$ — некоторый предок $$$v$$$ и $$$h(v) - k \le h(to)$$$.
В данной задаче считается, что корень не является листом (даже если его степень равна $$$1$$$). Посчитайте максимальное количество различных листов, которые вы сможете посетить одной последовательностью ходов.
В первой строке заданы два целых числа $$$n$$$ и $$$k$$$ ($$$1 \le k < n \le 10^6$$$) — количество вершин в дереве и ограничение на высоту подъема.
Вторая строка содержит $$$n - 1$$$ целых чисел $$$p_2, p_3, \dots, p_n$$$, где $$$p_i$$$ — непосредственный родитель вершины $$$i$$$.
Гарантируется, что входные данные задают дерево с корнем в вершине $$$1$$$.
Выведите единственное целое число — максимально возможное количество различных листов, которые вы сможете посетить одной последовательностью ходов.
7 1
1 1 3 3 4 4
4
8 2
1 1 2 3 4 5 5
2
Граф из первого примера изображен ниже:
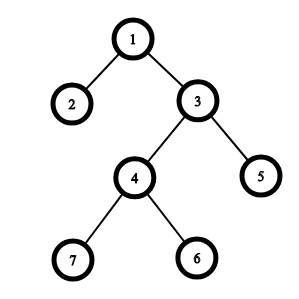
Один из возможных оптимальных обходов: $$$1 \rightarrow 2 \rightarrow 1 \rightarrow 5 \rightarrow 3 \rightarrow 7 \rightarrow 4 \rightarrow 6$$$.
Граф из второго примера:
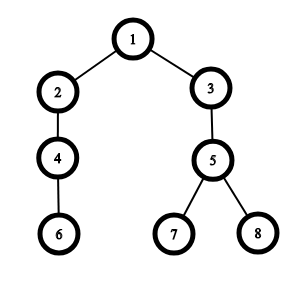
Один из возможных оптимальных обходов: $$$1 \rightarrow 7 \rightarrow 5 \rightarrow 8$$$. Заметим, что невозможно добраться из вершины $$$6$$$ в $$$7$$$ или $$$8$$$ и наоборот.
| Название |
|---|




