Многие мечтают о кабриолете. Некоторые кабриолеты, впрочем, вообще не имеют крыши (у остальных крыша складная). Поэтому известный изобретатель Мелон Аск решил разработать защиту от дождя для кабриолетов.
Рабочее пространство данного механизма расположено над головой водителя. Его главная часть — две параллельные рейки, по которым двигаются выступы, на которые, в свою очередь, натянута растяжимая верёвка. Для простоты представим эту констукцию в виде пары параллельных отрезков на плоскости, на каждом отрезке есть по точке, которые являются концами отрезка; и эти точки можно двигать по рейкам-отрезкам.
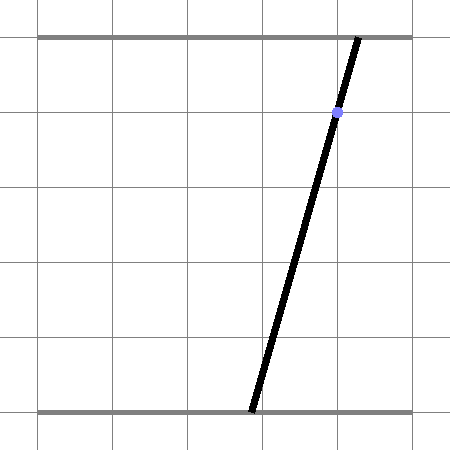
Алгоритмическая составляющая этого механизма обнаруживает капли дождя, летящие в кабриолет, и определяет, где и когда они будут в рабочей плоскости механизма. Для каждой дождинки в заданный момент верёвка должна проходить через заданную точку плоскости (и, таким образом, впитать в себя каплю).
Вам дано начальное положение верёвки, а также вся информация о каплях дождя. Ваша цель — найти такую минимальную скорость $$$v$$$, что можно собрать все капли, передвигая концы верёвки по рейкам со скоростью не больше $$$v$$$, или определить, что, как бы быстро мы ни двигали концы, нам не удастся собрать все капли.
Первая строка содержит три целых числа $$$n$$$, $$$w$$$ и $$$h$$$ ($$$1 \le n \le 10^5$$$, $$$1\le w, h \le 10^3$$$): число капель дождя $$$n$$$ и прямоугольник, задающий рейки. Одна рейка представлена отрезком с концами $$$(0, 0)$$$ и $$$(w, 0)$$$, а вторая — с концами $$$(0, h)$$$ и $$$(w, h)$$$.
Вторая строка содержит два целых числа $$$e_1$$$ и $$$e_2$$$, означающие, что изначально (в момент времени $$$t = 0$$$) концы верёвки находятся в точках $$$(e_1, 0)$$$ и $$$(e_2, h)$$$ ($$$0\le e_1, e_2\le w$$$).
$$$i$$$-я из следующих $$$n$$$ строк содержит по три целых числа $$$t_i$$$, $$$x_i$$$ и $$$y_i$$$ ($$$1\le t_i\le 10^5$$$, $$$0\le x_i \le w$$$, $$$0 < y_i < h$$$), означающих, что $$$i$$$-я капля попадёт в точку $$$(x_i, y_i)$$$ плоскости в момент времени $$$t_i$$$. Гарантируется, что $$$t_i \le t_{i+1}$$$ для всех $$$i$$$.
Если невозможно собрать все капли, выведите $$$-1$$$.
В противном случае выведите наименьшую скорость, с которой можно двигать концы верёвки и собрать все капли. Ваш ответ будет считаться верным, если его абсолютная или относительная погрешность не превосходит $$$10^{-4}$$$.
Формально, пусть ваш ответ равен $$$a$$$, а ответ жюри равен $$$b$$$. Ваш ответ будет зачтен, если $$$\frac{|a - b|}{\max{(1, |b|)}} \le 10^{-4}$$$.
3 5 5
0 0
1 1 4
2 2 4
3 3 4
1.0000000019
2 5 5
0 0
2 4 1
3 1 4
2.1428571437
3 5 5
0 0
1 2 1
1 3 3
1 4 2
-1
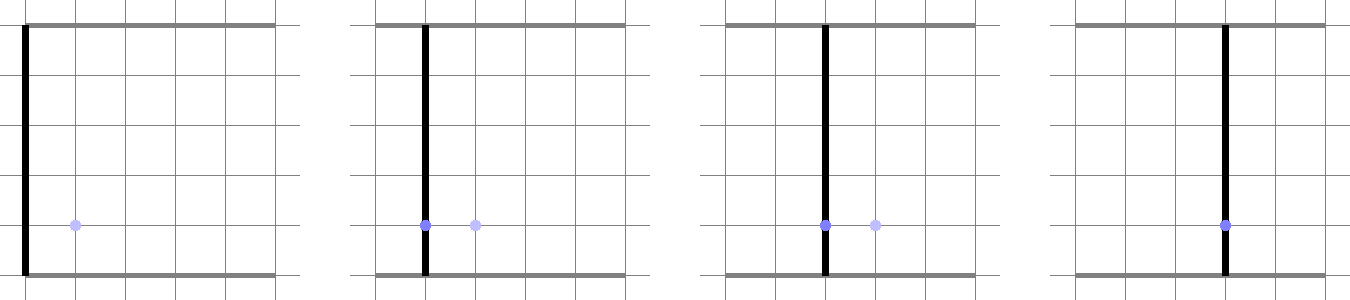
В первом тесте из условия действовать можно так:
Во втором так:
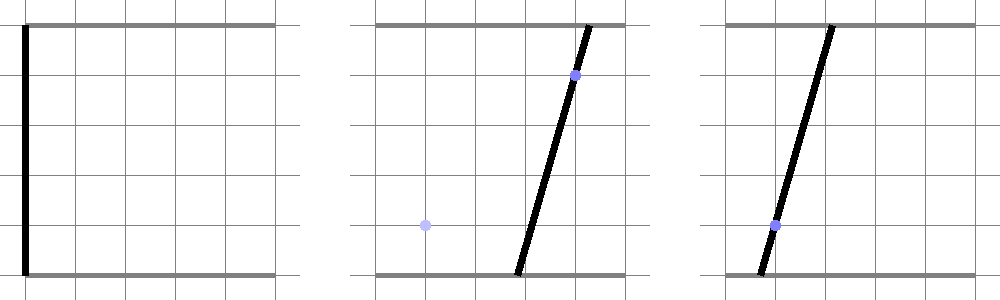
| Название |
|---|




