| Codeforces Round 526 (Div. 1) |
|---|
| Закончено |
Орехус отправляется путешествовать в Древесную страну, в которой $$$n$$$ городов. Кроме того, что большая часть её территории покрыта лесами, местная система дорог также представляет собой дерево (связный ациклический граф). Орехус хочет арендовать автомобиль в городе $$$u$$$ и поехать по простому пути до города $$$v$$$. Он ещё не определил свой путь, и сейчас самое время это сделать. Обратите внимание, что выбранный путь может состоять из одной вершины.
В $$$i$$$-м городе стоит бензоколонка, в которой по странным законам Древесной страны можно купить не более $$$w_i$$$ литров бензина. Можно считать, что у Орехуса бесконечное количество денег. У каждой дороги есть длина, и как только Орехус проезжает по ней, количество бензина уменьшается на длину дороги. Конечно, Орехус не сможет поехать по пути, на одной из дорог которого ему не хватит бензина. Он может купить в бензин в любом городе, в котором он был, в том числе в первом и последнем.
Кроме того, он хочет найти максимальное количество бензина, которое у него может остаться в конце пути. Помогите ему: посчитайте это количество.
Первая строка содержит одно целое число $$$n$$$ ($$$1 \leq n \leq 3 \cdot 10^5$$$) — количество городов.
Вторая строка содержит $$$n$$$ целых чисел $$$w_1, w_2, \ldots, w_n$$$ ($$$0 \leq w_{i} \leq 10^9$$$) — максимальные количества бензина, которое Орехус может купить в городах.
Каждая из следующих $$$n - 1$$$ строк описывает дорогу и содержит три целых числа $$$u$$$, $$$v$$$, $$$c$$$ ($$$1 \leq u, v \leq n$$$, $$$1 \leq c \leq 10^9$$$, $$$u \ne v$$$), где $$$u$$$ и $$$v$$$ — города, которые соединяет дорога, а $$$c$$$ — её длина.
Гарантируется, что граф соединённости городов дорогами - это правильное дерево.
Выведите одно число — максимальное количество бензина, которое может остаться у Орехуса в конце пути.
3
1 3 3
1 2 2
1 3 2
3
5
6 3 2 5 0
1 2 10
2 3 3
2 4 1
1 5 1
7
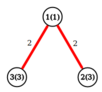
Оптимальный путь в первом примере $$$2 \to 1 \to 3$$$.
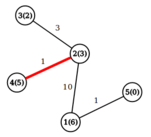
Оптимальный путь во втором примере $$$2 \to 4$$$.
| Название |
|---|




