| Codeforces Round 546 (Div. 2) |
|---|
| Finished |
Finished her homework, Nastya decided to play computer games. Passing levels one by one, Nastya eventually faced a problem. Her mission is to leave a room, where a lot of monsters live, as quickly as possible.
There are $$$n$$$ manholes in the room which are situated on one line, but, unfortunately, all the manholes are closed, and there is one stone on every manhole. There is exactly one coin under every manhole, and to win the game Nastya should pick all the coins. Initially Nastya stands near the $$$k$$$-th manhole from the left. She is thinking what to do.
In one turn, Nastya can do one of the following:
- if there is at least one stone on the manhole Nastya stands near, throw exactly one stone from it onto any other manhole (yes, Nastya is strong).
- go to a neighboring manhole;
- if there are no stones on the manhole Nastya stays near, she can open it and pick the coin from it. After it she must close the manhole immediately (it doesn't require additional moves).
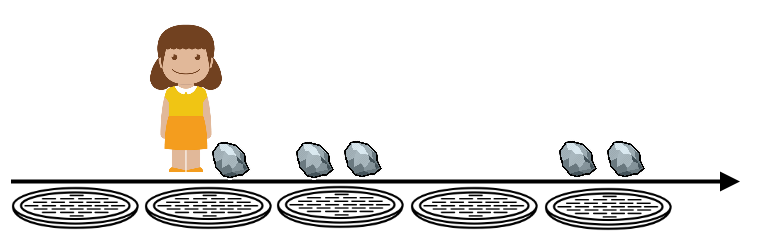 The figure shows the intermediate state of the game. At the current position Nastya can throw the stone to any other manhole or move left or right to the neighboring manholes. If she were near the leftmost manhole, she could open it (since there are no stones on it).
The figure shows the intermediate state of the game. At the current position Nastya can throw the stone to any other manhole or move left or right to the neighboring manholes. If she were near the leftmost manhole, she could open it (since there are no stones on it). Nastya can leave the room when she picks all the coins. Monsters are everywhere, so you need to compute the minimum number of moves Nastya has to make to pick all the coins.
Note one time more that Nastya can open a manhole only when there are no stones onto it.
The first and only line contains two integers $$$n$$$ and $$$k$$$, separated by space ($$$2 \leq n \leq 5000$$$, $$$1 \leq k \leq n$$$) — the number of manholes and the index of manhole from the left, near which Nastya stays initially. Initially there is exactly one stone near each of the $$$n$$$ manholes.
Print a single integer — minimum number of moves which lead Nastya to pick all the coins.
2 2
6
4 2
13
5 1
15
Let's consider the example where $$$n = 2$$$, $$$k = 2$$$. Nastya should play as follows:
- At first she throws the stone from the second manhole to the first. Now there are two stones on the first manhole.
- Then she opens the second manhole and pick the coin from it.
- Then she goes to the first manhole, throws two stones by two moves to the second manhole and then opens the manhole and picks the coin from it.
So, $$$6$$$ moves are required to win.
| Name |
|---|




