Вам дано корневое дерево с $$$n$$$ вершинами, пронумерованными от $$$1$$$ до $$$n$$$. Корнем дерева является вершина $$$1$$$. Предком $$$i$$$-й вершины является вершина $$$p_i$$$. Лист — это вершина без детей. Для некоторого набора листьев $$$L$$$ пусть $$$f(L)$$$ обозначает наименьший связный подграф, содержащий все листья $$$L$$$.
Вы хотите разделить листы так, чтобы для любых двух различных множеств $$$x, y$$$ разбиения $$$f(x)$$$ и $$$f(y)$$$ не пересекались.
Подсчитайте количество способов разбить листья по модулю $$$998244353$$$. Два разбиения различны, если есть такие два листа, которые находятся в одном множестве в одному разбиении, а в другом в двух различных.
Первая строка содержит одно целое число $$$n$$$ ($$$2 \leq n \leq 200\,000$$$) — количество вершин в дереве.
Вторая строка содержит $$$n-1$$$ целых чисел $$$p_2, p_3, \ldots, p_n$$$ ($$$1 \leq p_i < i$$$).
Выведите одно целое число по модулю $$$998244353$$$ — количество способов разбить вершины.
5 1 1 1 1
12
10 1 2 3 4 5 6 7 8 9
1
В первом примере листьями являются вершины $$$2,3,4,5$$$. Способы разделить листья: 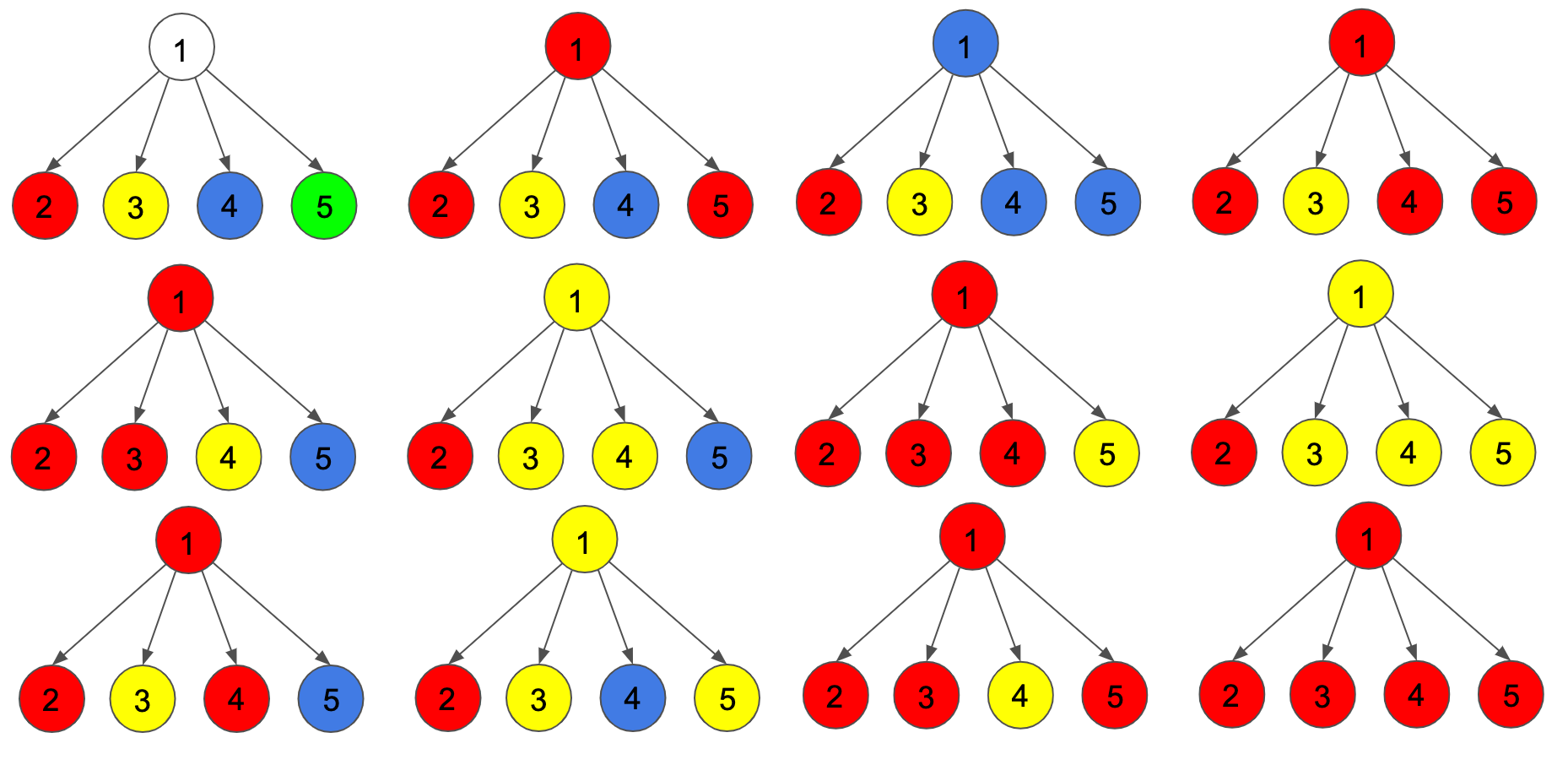
Во втором примере есть только один лист $$$10$$$. Значит, что есть только один способ разбиения. Обратите внимание, что вершина $$$1$$$ не является листом.
| Название |
|---|




