У вас есть список чисел от $$$1$$$ по $$$n$$$, записанных слева направо на доске.
Вы выполняете алгоритм, состоящий из нескольких шагов (шаги нумеруются с $$$1$$$). На $$$i$$$-м шаге вы стираете $$$i$$$-е число (вы учитываете только оставшиеся числа). Вы стираете с доски число полностью (а не только одну цифру).
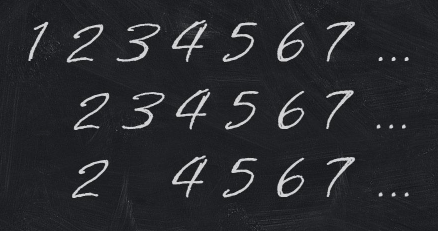
Когда на доске осталось меньше, чем $$$i$$$ чисел, вы прекращаете выполнение алгоритма.
Вам стало интересно: чему равно $$$x$$$-е оставшееся число после завершения алгоритма?
В первой строке задано одно число $$$T$$$ ($$$1 \le T \le 100$$$) — количество запросов. Следующие $$$T$$$ строк содержат сами запросы — по одному в строке. Все запросы независимы.
Каждая строка содержит два целых числа $$$n$$$ и $$$x$$$ ($$$1 \le x < n \le 10^{9}$$$) — длину списка и позицию, о которой мы хотим узнать. Гарантируется, что после завершения алгоритма, список будет содержать хотя бы $$$x$$$ чисел.
Выведите $$$T$$$ чисел (по одному на запрос) — значения $$$x$$$-х чисел после завершения алгоритма для соответствующих запросов.
3 3 1 4 2 69 6
2 4 12
| Название |
|---|




