Вам задан набор из n векторов на плоскости. Для каждого вектора разрешается домножить любые его координаты на -1. Таким образом, каждый вектор vi = (xi, yi) можно преобразовать в один из следующих четырех векторов:
- vi1 = (xi, yi),
- vi2 = ( - xi, yi),
- vi3 = (xi, - yi),
- vi4 = ( - xi, - yi).
Вам нужно найти два вектора из набора и определить, какие из их координат следует умножить на -1 таким образом, чтобы модуль суммы полученных векторов был минимально возможным. Более формально, требуется выбрать два вектора vi, vj (1 ≤ i, j ≤ n, i ≠ j) и два числа k1, k2 (1 ≤ k1, k2 ≤ 4), так чтобы значение выражения |vik1 + vjk2| было минимально.
В первой строке записано одно целое число n (2 ≤ n ≤ 105). Далее в n строках записаны вектора в виде пар целых чисел «xi yi» ( - 10000 ≤ xi, yi ≤ 10000), по одной паре в строке.
Выведите в первой строке четыре числа через пробел «i k1 j k2» — ответ на задачу. Если существует несколько вариантов с минимальным модулем суммы, можете вывести любой из них.
5
-7 -3
9 0
-8 6
7 -8
4 -5
3 2 4 2
5
3 2
-4 7
-6 0
-8 4
5 1
3 4 5 4
Суммой двух векторов v = (xv, yv) и u = (xu, yu) называется вектор s = v + u = (xv + xu, yv + yu).
Модулем вектора v = (x, y) называется число 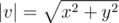 .
.
Во втором примере существует несколько подходящих ответов, вот некоторые из них:
(3 1 4 2), (3 1 4 4), (3 4 4 1), (3 4 4 3), (4 1 3 2), (4 1 3 4), (4 2 3 1).
| Название |
|---|




