| Codeforces Round 580 (Div. 1) |
|---|
| Finished |
You are given integer $$$n$$$. You have to arrange numbers from $$$1$$$ to $$$2n$$$, using each of them exactly once, on the circle, so that the following condition would be satisfied:
For every $$$n$$$ consecutive numbers on the circle write their sum on the blackboard. Then any two of written on the blackboard $$$2n$$$ numbers differ not more than by $$$1$$$.
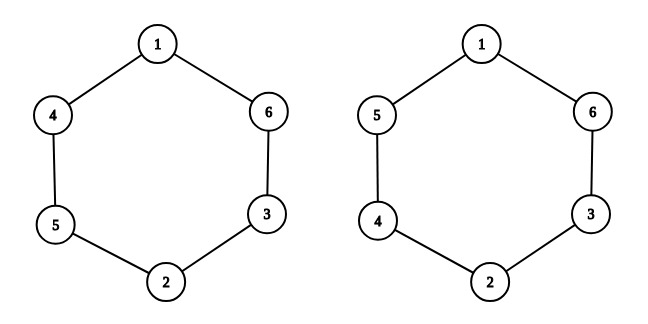
For example, choose $$$n = 3$$$. On the left you can see an example of a valid arrangement: $$$1 + 4 + 5 = 10$$$, $$$4 + 5 + 2 = 11$$$, $$$5 + 2 + 3 = 10$$$, $$$2 + 3 + 6 = 11$$$, $$$3 + 6 + 1 = 10$$$, $$$6 + 1 + 4 = 11$$$, any two numbers differ by at most $$$1$$$. On the right you can see an invalid arrangement: for example, $$$5 + 1 + 6 = 12$$$, and $$$3 + 2 + 4 = 9$$$, $$$9$$$ and $$$12$$$ differ more than by $$$1$$$.
The first and the only line contain one integer $$$n$$$ ($$$1 \le n \le 10^5$$$).
If there is no solution, output "NO" in the first line.
If there is a solution, output "YES" in the first line. In the second line output $$$2n$$$ numbers — numbers from $$$1$$$ to $$$2n$$$ in the order they will stay in the circle. Each number should appear only once. If there are several solutions, you can output any of them.
3
YES 1 4 5 2 3 6
4
NO
Example from the statement is shown for the first example.
It can be proved that there is no solution in the second example.
| Name |
|---|




