A. Почти равные
ограничение по времени на тест
1 секунда
ограничение по памяти на тест
256 мегабайт
ввод
стандартный ввод
вывод
стандартный вывод

Дано целое положительное число $$$n$$$. Нужно расставить числа от $$$1$$$ до $$$2n$$$ по кругу таким образом, чтобы выполнялось следующее условие:

Для каждых $$$n$$$ последовательных чисел на окружности выпишем на доску их сумму. Тогда любые два из выписанных на доске $$$2n$$$ чисел отличаются не более, чем на $$$1$$$.

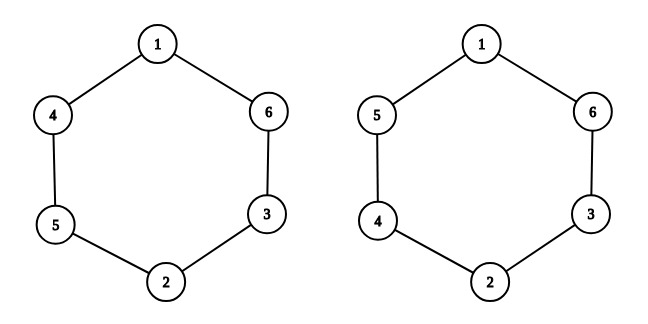
К примеру, выберем $$$n = 3$$$. Слева вы можете увидеть пример правильной расстановки:$$$1 + 4 + 5 = 10$$$, $$$4 + 5 + 2 = 11$$$, $$$5 + 2 + 3 = 10$$$, $$$2 + 3 + 6 = 11$$$, $$$3 + 6 + 1 = 10$$$, $$$6 + 1 + 4 = 11$$$, любые два числа отличаются не более чем на $$$1$$$. Справа вы можете увидеть неправильную расстановку: к примеру, $$$5 + 1 + 6 = 12$$$, а $$$3 + 2 + 4 = 9$$$, $$$9$$$ и $$$12$$$ отличаются более чем на $$$1$$$.

Входные данные

Первая и единственная строка содержит одно целое число $$$n$$$ ($$$1 \le n \le 10^5$$$).

Выходные данные

Если решения не существует, в первой строке выведите «NO».

Если оно существует, в первой строке выведите «YES». После чего, во второй строке выведите $$$2n$$$ чисел — числа от $$$1$$$ до $$$2n$$$ в порядке в котором они будут стоять на окружности. Каждое число должно встречаться только один раз. Если есть несколько решений, выведите любое.

Примеры
Входные данные
3
Выходные данные
YES
1 4 5 2 3 6
Входные данные
4
Выходные данные
NO
Примечание

Пример из условия приведен для первого примера.

Можно доказать, что для второго примера решения не существует.