Введем определение хорошего мультимножества следующим образом. Выпишем сумму всех элементов мультимножества в виде десятичного числа. Если для каждого разряда существует хотя бы одно число из мультимножества, в котором такая же цифра, как и в полученной сумме, то мультимножество хорошее, иначе плохое.
Например, мультимножество $$$\{20, 300, 10001\}$$$ — хорошее, а мультимножество $$$\{20, 310, 10001\}$$$ — плохое:
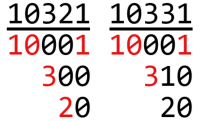
Красным отмечены те числа и разряды, в которых те же цифры, что и в сумме. Сумма первого мультимножества равна $$$10321$$$, для каждого разряда есть необходимая цифра. Сумма второго мультимножества равна $$$10331$$$, и для второго с конца разряда не сушествует числа с такой же цифрой, что делает мультимножество плохим.
Вам дан массив из $$$n$$$ целых чисел $$$a_1, a_2, \dots, a_n$$$.
Необходимо ответить на запросы к нему. Запросы могут быть двух типов:
- $$$1~i~x$$$ — заменить $$$a_i$$$ на $$$x$$$;
- $$$2~l~r$$$ — найти плохое подмножество мультимножества чисел $$$a_l, a_{l + 1}, \dots, a_r$$$ с минимальной суммой или сказать, что плохих подмножеств не существует.
Обратите внимание, что пустое подмножество является хорошим.
Для каждого запроса второго типа выведите наименьшую сумму плохого подмножества. Выведите -1, если не существует плохого подмножества.
В первой строке записаны два целых числа $$$n$$$ и $$$m$$$ ($$$1 \le n, m \le 2 \cdot 10^5$$$) — количество элементов в массиве и количество запросов, соответственно.
Во второй строке записаны $$$n$$$ целых чисел $$$a_1, a_2, \dots, a_n$$$ ($$$1 \le a_i < 10^9$$$).
В каждой из следующих $$$m$$$ строк записан запрос одного из двух типов:
- $$$1~i~x$$$ ($$$1 \le i \le n$$$, $$$1 \le x < 10^9$$$) — заменить $$$a_i$$$ на $$$x$$$;
- $$$2~l~r$$$ ($$$1 \le l \le r \le n$$$) — найти плохое подмножество мультимножества чисел $$$a_l, a_{l + 1}, \dots, a_r$$$ с минимальной суммой или сказать, что плохих подмножеств не существует.
Гарантируется, что есть хотя бы один запрос второго типа.
Для каждого запроса второго типа выведите наименьшую сумму плохого подмножества. Выведите -1, если не существует плохого подмножества.
4 5 300 10001 20 20 2 1 3 1 1 310 2 1 3 2 3 3 2 3 4
-1 330 -1 40
Все подмножества мультимножества $$$\{20, 300, 10001\}$$$ являются хорошими, поэтому ответ -1.
Все возможные плохие подмножества в третьем запросе: $$$\{20, 310\}$$$ и $$$\{20, 310, 10001\}$$$. С меньшей суммой — $$$\{20, 310\}$$$. Обратите внимание, что требуется найти подмножество, а не подотрезок, поэтому выбранные элементы не обязательно будут стоять рядом в массиве.
В четвертом запросе есть только пустое подножество и подмножество $$$\{20\}$$$. Оба они хорошие.
В последнем запросе есть пустое подмножество и подмножества $$$\{20\}$$$, $$$\{20\}$$$ и $$$\{20, 20\}$$$. Только $$$\{20, 20\}$$$ — плохое, его сумма равна $$$40$$$. Обратите внимание, что требуется выбрать мультимножество, поэтому оно может включать в себя одинаковые элементы.
| Название |
|---|




