| Codeforces Round 593 (Div. 2) |
|---|
| Закончено |
У Алисы недавно появилась новая кукла. Она даже может ходить!
Алиса построила лабиринт для куклы и хочет протестировать его. Лабиринт имеет вид таблицы с $$$n$$$ строками и $$$m$$$ столбцами. Также есть $$$k$$$ препятствий, $$$i$$$-е из них находится в клетке $$$(x_i, y_i)$$$, это клетка на пересечении строки с номером $$$x_i$$$ и столбца с номером $$$y_i$$$.
Однако кукла очень неуклюжая. Она может только идти прямо и поворачиваться направо, но не больше одного раза в одной клетке (включая стартовую клетку). Она не может переходить в клетку с препятствием, а также покидать пределы лабиринта.
Более формально, всего существует $$$4$$$ направления, в которых может смотреть кукла:
- Кукла смотрит в направлении вдоль строки от первой клетки к последней. Перемещаясь смотря в этом направлении, кукла переходит из клетки $$$(x, y)$$$ в клетку $$$(x, y + 1)$$$;
- Кукла смотрит в направлении вдоль столбца от первой клетки к последней. Перемещаясь смотря в этом направлении, кукла переходит из клетки $$$(x, y)$$$ в клетку $$$(x + 1, y)$$$;
- Кукла смотрит в направлении вдоль строки от последней клетки к первой. Перемещаясь смотря в этом направлении, кукла переходит из клетки $$$(x, y)$$$ в клетку $$$(x, y - 1)$$$;
- Кукла смотрит в направлении вдоль столбца от последней клетки к первой. Перемещаясь смотря в этом направлении, кукла переходит из клетки$$$(x, y)$$$ в клетку $$$(x - 1, y)$$$.
Находясь в некоторой клетке, кукла может перейти в клетку в направлении, в котором она смотрит, либо повернуться один раз направо. Поворачиваясь один раз направо, кукла меняет направление, в котором она смотрит следующим образом: $$$1 \to 2$$$, $$$2 \to 3$$$, $$$3 \to 4$$$, $$$4 \to 1$$$. В одной клетке, кукла может совершить не более одного поворота направо.
Сейчас Алиса управляет перемещениями куклы. Изначально она поставила куклу в клетку $$$(1, 1)$$$ (верхняя левая клетка лабиринта). Изначально кукла смотрит в направлении $$$1$$$, то есть в направлении вдоль строки от первой клетки к последней. Она хочет обойти куклой все клетки лабиринта, не содержащие препятствий ровно по одному разу и закончить в любой клетке. Существует ли способ так сделать?
В первой строке находится три целых числа $$$n$$$, $$$m$$$ и $$$k$$$, разделенных пробелами ($$$1 \leq n,m \leq 10^5, 0 \leq k \leq 10^5$$$) — размеры лабиринта и количество препятствий.
В следующих $$$k$$$ строках находится описание препятствий, $$$i$$$-я из этих строк содержит два целых числа $$$x_i$$$ и $$$y_i$$$, разделенные пробелом ($$$1 \leq x_i \leq n,1 \leq y_i \leq m$$$), которые описывают позицию $$$i$$$-го препятствия.
Гарантируется, что никакие два препятствия не находятся в одной клетке и что нету препятствия в клетке $$$(1, 1)$$$.
Выведите 'Yes' (без кавычек) если кукла может обойти все клетки, не содержащие препятствий по описанным выше правилам ровно по одному разу.
Если так обойти лабиринт невозможно, выведите 'No' (без кавычек).
3 3 2 2 2 2 1
Yes
3 3 2 3 1 2 2
No
3 3 8 1 2 1 3 2 1 2 2 2 3 3 1 3 2 3 3
Yes
Картинка с лабиринтом из первого примера:
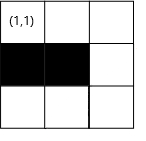
В первом примере, кукла может идти по следующему пути:
- Кукла в клетке $$$(1, 1)$$$, смотрит в направлении $$$1$$$. Пройти прямо;
- Кукла в клетке $$$(1, 2)$$$, смотрит в направлении $$$1$$$. Пройти прямо;
- Кукла в клетке $$$(1, 3)$$$, смотрит в направлении $$$1$$$. Повернуть направо;
- Кукла в клетке $$$(1, 3)$$$, смотрит в направлении $$$2$$$. Пройти прямо;
- Кукла в клетке $$$(2, 3)$$$, смотрит в направлении $$$2$$$. Пройти прямо;
- Кукла в клетке $$$(3, 3)$$$, смотрит в направлении $$$2$$$. Повернуть направо;
- Кукла в клетке $$$(3, 3)$$$, смотрит в направлении $$$3$$$. Пройти прямо;
- Кукла в клетке $$$(3, 2)$$$, смотрит в направлении $$$3$$$. Пройти прямо;
- Кукла в клетке $$$(3, 1)$$$, смотрит в направлении $$$3$$$. Цель достигнута, все клетки лабиринта, не содержащие препятствия посещены ровно один раз.
| Название |
|---|




