| Codeforces Round 594 (Div. 2) |
|---|
| Закончено |
Садовод Лёша преподаёт школьникам олимпиадную информатику. На день учителя ребята подарили ему набор деревянных палочек, каждая из которых представляет собой отрезок целочисленной длины. Теперь Лёша хочет вырастить из них дерево.
Дерево представляет собой ломаную на плоскости, состоящую из всех подаренных ему палочек. Ломаная начинается в точке $$$(0, 0)$$$. Строя ломаную, Лёша может присоединять палочки в любом порядке, располагая каждую горизонтально или вертикально (то есть параллельно оси $$$OX$$$ или $$$OY$$$). При этом не разрешается, чтобы две подряд идущие палочки лежали одновременно горизонтально или вертикально. Смотрите картинки ниже для уточнения деталей.
Лёша хочет сделать так, чтобы конец ломаной был как можно дальше от точки $$$(0, 0)$$$. Помогите ему вырастить дерево таким образом!
Заметим, что ломаная, в форме которой Леша вырастит дерево, может иметь самопересечения и самокасания, однако можно доказать, что оптимальный ответ не содержит ни самопересечений, ни самокасаний.
Первая строка содержит целое число $$$n$$$ ($$$1 \le n \le 100\,000$$$) — количество палочек, подаренных Лёше.
Вторая строка содержит $$$n$$$ целых чисел $$$a_1, \ldots, a_n$$$ ($$$1 \le a_i \le 10\,000$$$) — длины палочек, подаренных Лёше.
Выведите одно целое число — квадрат максимального расстояния от точки $$$(0, 0)$$$ до конечной точки дерева.
3 1 2 3
26
4 1 1 2 2
20
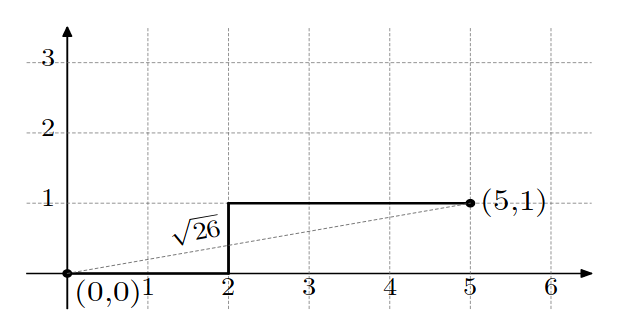
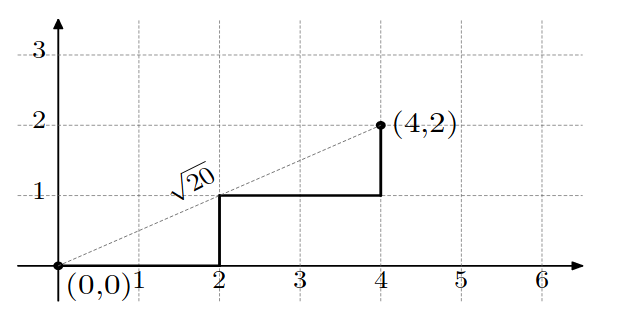
На следующих изображениях нарисованы оптимальные деревья для примеров из условия. Квадрат расстояния в первом случае равен $$$5 \cdot 5 + 1 \cdot 1 = 26$$$, а во втором $$$4 \cdot 4 + 2 \cdot 2 = 20$$$.
| Название |
|---|




