| Codeforces Global Round 6 |
|---|
| Закончено |
Боб играет со стандартными $$$6$$$-гранными костями (кубиками). Развертка стандартного кубика приведена на рисунке ниже.
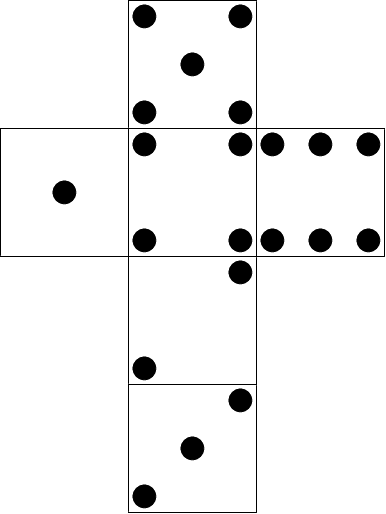
У Боба есть бесконечное число игральных кубиков, и он хочет построить из них башню, ставя один кубик на другой и выбирая ориентацию каждого нового кубика. После того, как Боб построит башню, он посчитает количество видимых точек на гранях кубиков.
Например, количество видимых точек на башне, нарисованной ниже, равно $$$29$$$ — число точек на верхней грани верхнего кубика равно $$$1$$$, а с четырех сторон башни видны грани со следующим количеством точек: $$$5$$$ и $$$3$$$ с южной стороны, $$$4$$$ и $$$2$$$ с западной стороны, $$$2$$$ и $$$4$$$ с северной стороны, и $$$3$$$ и $$$5$$$ с восточной стороны.
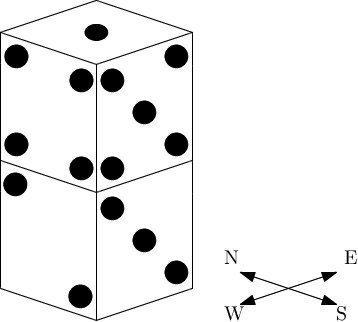
Нижняя грань первого кубика (с единицей) и грани с шестью точками не видны, поэтому они не учитываются в количестве видимых точек.
У Боба есть $$$t$$$ любимых чисел $$$x_i$$$. Для каждого из чисел $$$x_i$$$ помогите Бобу узнать, можно ли построить башню из кубиков, для которой количество видимых точек равно этому числу.
В первой строке задано одно целое число $$$t$$$ ($$$1 \leq t \leq 1000$$$) — количество любимых чисел Боба.
Во второй строке заданы $$$t$$$ целых чисел $$$x_i$$$ ($$$1 \leq x_i \leq 10^{18}$$$) — любимые числа Боба.
Для каждого любимого числа Боба выведите «YES», если можно построить башню, или «NO» в противном случае (без кавычек).
4 29 34 19 38
YES YES YES NO
Первый пример разобран в условии.
Ответ на второй пример можно получить, если перевернуть верхний кубик на башне из условия.
В третьем примере достаточно единственного кубика, поставленного таким образом, что на верхней грани изображено $$$5$$$ точек.
В четвертом примере не существует башни с нужным количеством видимых точек.
| Название |
|---|




