| Codeforces Round 628 (Div. 2) |
|---|
| Закончено |
Вам дано дерево, состоящее из $$$n$$$ вершин. Вы хотите написать какие-то числа на ребрах дерева, чтобы выполнялись следующие условия:
- Каждое написанное число является целым числом от $$$0$$$ до $$$n-2$$$ включительно.
- Все написанные числа различны.
- Наибольшее значение среди $$$MEX(u,v)$$$ среди всех пар вершин $$$(u,v)$$$ минимально возможно.
Здесь $$$MEX(u,v)$$$ обозначает наименьшее неотрицательное целое число, которое не записано ни на одном ребре уникального простого пути между вершинами $$$u$$$ и $$$v$$$.
В первой строке записано целое число $$$n$$$ ($$$2 \le n \le 10^5$$$) — количество узлов в дереве.
Каждая из следующих $$$n-1$$$ строк содержит два разделенных пробелом целых числа $$$u$$$ и $$$v$$$ ($$$1 \le u,v \le n$$$), которые означают, что между узлами $$$u$$$ и $$$v$$$ есть ребро. Гарантируется, что данный граф является деревом.
Выведите $$$n-1$$$ целых чисел. $$$i$$$-е из них должно быть равно числу, записанным на $$$i$$$-м ребре (в порядке ввода).
3 1 2 1 3
0 1
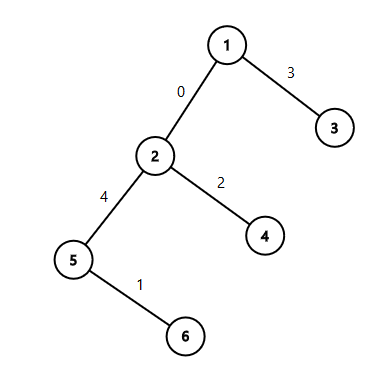
6 1 2 1 3 2 4 2 5 5 6
0 3 2 4 1
Дерево с второго примера:
| Название |
|---|




