Посчитайте количество способов расставить $$$n$$$ ладей на доске $$$n \times n$$$ так, что выполняются оба следующих условия:

• все пустые клетки атакованы;
• ровно $$$k$$$ пар ладей атакуют друг друга.

Пустая клетка считается атакованной, если хотя бы одна ладья находится в той же строке или в том же столбце. Две ладьи атакуют друг друга, если они находятся в одной и той же строке или в одном и том же столбце, и между ними нет других ладей. Например, на следующей картинке можно найти только две пары ладей, атакующих друг друга:

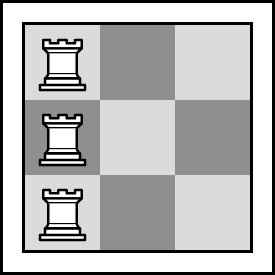Один из способов расставить ладьи при $$$n = 3$$$ и $$$k = 2$$$

Два способа считаются различными, если существует хотя бы одна клетка, которая свободна в одном из способов и занята ладьей в другом способе.

Ответ может быть очень большим, поэтому выведите его по модулю $$$998244353$$$.