У младшей сестры Джонни, Меган, недавно был день рождения. Её брат подарил ей коробочку, подписанную как: «Твое прекрасное ожерелье — сделай сама!». Коробочка содержит много частей ожерелья и магический клей.
Каждая часть ожерелья представляет собой цепочку, соединяющую две жемчужины. Цвет каждой из жемчужин может быть представлен целым неотрицательным числом. Магический клей позволяет Меган склеивать две жемчужины (возможно, из одной части ожерелья) в одну. Красота соединения двух жемчужин цветов $$$u$$$ и $$$v$$$ определяется следующим образом: пусть $$$2^k$$$ — максимальная степень двух, делящая $$$u \oplus v$$$ — исключающее или $$$u$$$ и $$$v$$$. Тогда красота соединения равна $$$k$$$. Если $$$u = v$$$, вы можете считать, что красота равна $$$20$$$.
Каждая жемчужина может быть склеена с другой максимум один раз. Склеивание двух частей ожерелья объединяет их. Используя клей несколько раз, Меган может наконец получить свое ожерелье, которое является циклом, сделанным из соединенных последовательно частей ожерелья (так, что каждая жемчужина в ожерелье соединена с ровно одной другой жемчужиной). Красота такого ожерелья равна минимальной красоте соединений в нем. Девочка хочет использовать все доступные части ожерелья, чтобы получить ровно одно ожерелье, содержащее все части, с максимальной возможной красотой. Помогите ей!
Первая строка содержит целое число $$$n$$$ $$$(1 \leq n \leq 5 \cdot 10^5)$$$ — количество частей ожерелья в коробочке.
Каждая из следующих $$$n$$$ строк содержит два целых числа $$$a$$$ и $$$b$$$ $$$(0 \leq a, b < 2^{20})$$$, которые обозначают цвета жемчужин из этой части ожерелья. Жемчужины на $$$i$$$-й строке имеют индексы $$$2i - 1$$$ и $$$2i$$$, соответственно.
Первая строка должна содержать одно целое число $$$b$$$, обозначающее максимальную возможную красоту ожерелья, собранного из всех данных частей.
Следующая строка должна содержать $$$2n$$$ различных целых чисел $$$p_i$$$ $$$(1 \leq p_i \leq 2n)$$$ — индексы исходных жемчужин в порядке, в котором они должны быть расположены в ожерелье. Индексы жемчужин, принадлежащих одной части, должны быть расположены на соседних позициях в перестановке (поэтому $$$1\,4\,3\,2$$$ не является корректным выводом, а $$$2\,1\,4\,3$$$ и $$$4\,3\,1\,2$$$ являются). Если существует несколько подходящих ответов, вы можете вывести любой.
5 13 11 11 1 3 5 17 1 9 27
3 8 7 9 10 5 6 1 2 3 4
5 13 11 11 1 3 5 17 1 7 29
2 8 7 10 9 5 6 4 3 2 1
1 1 1
20 2 1
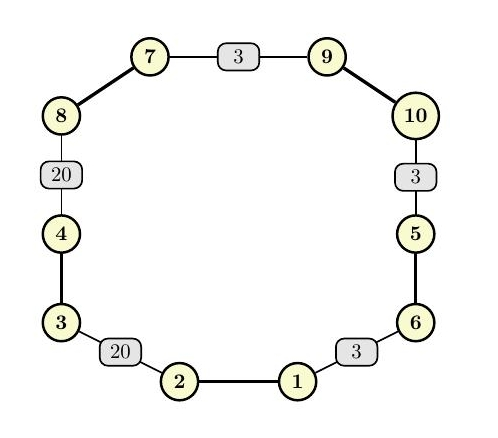
В первом примере следующие пары жемчужин объединяются: $$$(7, 9)$$$, $$$(10, 5)$$$, $$$(6, 1)$$$, $$$(2, 3)$$$ и $$$(4, 8)$$$. Красота соединений равна: $$$3$$$, $$$3$$$, $$$3$$$, $$$20$$$, $$$20$$$, соответственно.
Иллюстрация показывает эту конструкцию:
| Название |
|---|




