| Codeforces Round 665 (Div. 2) |
|---|
| Закончено |
Вам задана точка $$$A$$$ с координатой $$$x = n$$$ на оси $$$OX$$$. Вам хотелось бы найти такую целочисленную точку $$$B$$$ (также на оси $$$OX$$$), что модуль разности между расстоянием от $$$O$$$ до $$$B$$$ и расстоянием от $$$A$$$ до $$$B$$$ равен $$$k$$$.
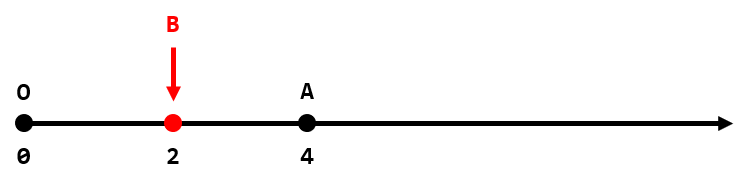 Описание первого набора входных данных.
Описание первого набора входных данных. Так как иногда невозможно найти такую точку $$$B$$$, вы можете за один шаг увеличить или уменьшить координату $$$A$$$ на $$$1$$$. Какое минимальное количество шагов необходимо сделать, чтобы такая точка $$$B$$$ существовала?
В первой строке задано одно целое число $$$t$$$ ($$$1 \le t \le 6000$$$) — количество наборов входных данных.
В единственной строке каждого набора заданы два целых числа $$$n$$$ и $$$k$$$ ($$$0 \le n, k \le 10^6$$$) — первоначальная позиция точки $$$A$$$ и желаемый модуль разности.
Для каждого набора входных данных, выведите минимальное количество шагов, необходимых для существования точки $$$B$$$.
6 4 0 5 8 0 1000000 0 0 1 0 1000000 1000000
0 3 1000000 0 1 0
В первом наборе входных данных (изображение выше), если мы выберем координату $$$B$$$ как $$$2$$$, то модуль разности будет равен $$$|(2 - 0) - (4 - 2)| = 0$$$ и нам не нужно передвигать $$$A$$$. Поэтому ответ равен $$$0$$$.
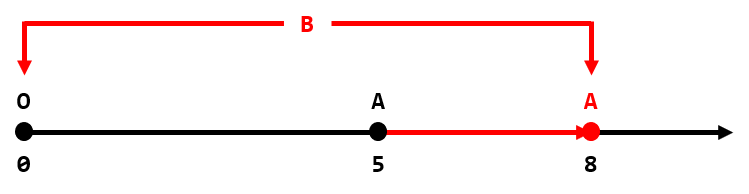
Во втором наборе входных данных, мы можем увеличить координату $$$A$$$ на $$$3$$$ и выбрать координату $$$B$$$ как $$$0$$$ или $$$8$$$. Модуль разности в таком случае будет равен $$$|8 - 0| = 8$$$, то есть ответ равен $$$3$$$.
| Название |
|---|




