| Codeforces Round 674 (Div. 3) |
|---|
| Закончено |
У Маши есть $$$n$$$ типов плиток размера $$$2 \times 2$$$. В каждой из четырех клеток плитки записано по одному целому числу. У Маши есть неограниченное количество плиток каждого из типов.
Маша решила выложить из своих плиток квадрат размера $$$m \times m$$$, причем этот квадрат должен представлять из себя симметричную относительно главной диагонали матрицу, а каждая клетка квадрата должна быть покрыта ровно одной клеткой плитки, причем боковые стороны плиток после укладки должны быть параллельны боковым сторонам квадрата. Уложенные плитки не должны пересекаться между собой. Также плитки должны целиком лежать внутри квадрата. Рассмотрите рисунок из примечания для лучшего понимания условия.
Симметричная относительно главной диагонали матрица — это квадрат $$$s$$$, у которого для всех пар $$$(i, j)$$$ верно, что $$$s[i][j] = s[j][i]$$$. То есть для всех клеток верно, что элемент, записанный на пересечении $$$i$$$-й строки и $$$j$$$-го столбца равен элементу, который записан на пересечении $$$j$$$-й строки и $$$i$$$-го столбца.
Перед вами стоит задача определить, сможет ли Маша выложить из своих плиток квадрат размера $$$m \times m$$$, который будет представлять из себя симметричную матрицу. Для укладки Маша может использовать неограниченное количество плиток каждого из имеющихся у нее типов. Обратите внимание, что плитки нельзя поворачивать, их можно укладывать только в той ориентации, в которой они заданы во входных данных.
Вам необходимо ответить на $$$t$$$ независимых наборов тестовых данных.
Первая строка содержит одно целое число $$$t$$$ ($$$1 \le t \le 100$$$) — количество наборов тестовых данных. Затем следуют $$$t$$$ наборов тестовых данных.
Первая строка набора тестовых данных содержит два целых числа $$$n$$$ и $$$m$$$ ($$$1 \le n \le 100$$$, $$$1 \le m \le 100$$$) — количество типов плиток и размер квадрата, который хочет выложить Маша.
Следующие $$$2n$$$ строк набора тестовых данных содержит описание типов плиток. Типы плиток описываются по очереди, на каждый тип отведено по две строки.
Сначала следует два целых положительных числа, не превосходящих $$$100$$$ — число, записанное в левом верхнем углу плитки очередного типа, и число, записанное в правом верхнем углу плитки очередного типа. В следующей строке следует два целых положительных числа, не превосходящих $$$100$$$ — число, записанное в левом нижнем углу плитки очередного типа, и число, записанное в правом нижнем углу плитки очередного типа.
В ходе укладки плитки запрещено поворачивать, их можно укладывать только в той ориентации, в которой они заданы во входных данных.
Выведите ответ на каждый набор тестовых данных: если Маша может выложить из своих плиток квадрат размера $$$m \times m$$$, который будет являться симметричной матрицей, выведите «YES» (без кавычек). В противном случае выведите «NO» (без кавычек).
6 3 4 1 2 5 6 5 7 7 4 8 9 9 8 2 5 1 1 1 1 2 2 2 2 1 100 10 10 10 10 1 2 4 5 8 4 2 2 1 1 1 1 1 2 3 4 1 2 1 1 1 1
YES NO YES NO YES YES
В первом наборе тестовых данных есть три типа плиток, они изображены на рисунке.
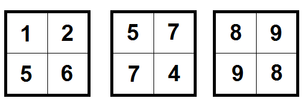
Из таких типов плиток можно составить, например, такой квадрат размера $$$4 \times 4$$$, который является симметричной матрицей:
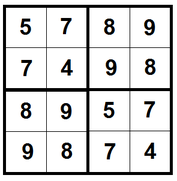
| Название |
|---|




