Это интерактивная задача
Женя сдает экзамен по теории игр. Так как профессору за много лет надоело слушать ответы на одни и те же билеты, вместо обычного экзамена он предложил Жене сыграть в игру.
Как известно из курса, комбинаторной игрой на графе с несколькими начальными позициями называется игра, в которой задан ориентированный граф и несколько начальных позиций в нем, в каждой из которых расположено по фишке. Два игрока по очереди двигают одну из фишек вдоль ребра графа. Тот игрок, который не может сделать ход, проигрывает. В случае, если оба игрока могут обеспечить сколь угодно длинную игру без своего поражения, объявляется ничья.
Для проведения экзамена профессор нарисовал на доске ацикличный ориентированный граф и загадал вершину в нем. Жене необходимо узнать загаданную вершину. Для этого он может несколько раз выбрать мультимножество вершин $$$S$$$ и задать профессору вопрос «Если поставить в каждую вершину графа столько фишек, сколько раз она в входит в мультимножество $$$S$$$, и еще одну фишку в загаданную вершину, то какой будет результат у такой комбинаторной игры?».
Рассказав задание, професор вышел из аудитории, чтобы Женя мог подготовиться к сдаче экзамена. Женя считает, что профессор хочет его обмануть, и выполнить задание невозможно. По этому, он хочет, пока профессор отошел, дорисовать в граф или удалить из графа несколько ребер. Несмотря на то, что исходный граф был ацикличным, после добавления ребер в графе могут появиться циклы.
Помогите Жене изменить граф так, чтобы он справился с заданием профессора.
Общение с интерактором в этой задаче состоит из нескольких фаз.
В первой фазе интерактор подает на ввод вашей программе три числа $$$N$$$ ($$$1 \le N \le 1000$$$), $$$M$$$ ($$$0 \le M \le 100\,000$$$), $$$T$$$ ($$$1 \le T \le 2000$$$) — количество вершин и ребер в исходном графе, а так же количество раз, которое надо отгадать загаданную вершину. В следующих $$$M$$$ строках записаны пары вершин $$$a_i$$$ $$$b_i$$$ ($$$1 \le a_i, b_i \le N$$$) — начало и конец соответствующего ребра графа. Гарантируется, что данный граф является ацикличным, и все ребра различны.
В ответ решение должно напечатать число $$$K$$$ ($$$0 \le K \le 4242$$$) — количество ребер, которое оно хочет изменить в графе. После этого надо напечатать $$$K$$$ строк, в каждой из которых будет написано либо «+ $$$a_i$$$ $$$b_i$$$», либо «- $$$a_i$$$ $$$b_i$$$» — начало и конец ребра, которое решение хочет добавить или удалить из графа соответственно. В граф можно добавлять ребра, которые там уже есть. Операции применяются в порядке вывода, можно удалять ребра, которое решение само добавило. Удаляемое ребро должно быть в графе. Граф может перестать быть ацикличным от этих операций.
После этого происходит $$$T$$$ фаз отгадывания вершины. В каждой фазе решение может сделать не более 20 запросов, после чего прислать ответ. Для того, чтобы задать вопрос про мультимножество $$$S$$$, нужно напечатать «? $$$|S|~S_1~S_2~\dots~S_{|S|}$$$». Суммарный размер мультимножеств на одной фазе не должен превосходить 20. В ответ интерактор напечатает одно из слов
- «Win», если в комбинаторной игре с фишками в мультимножестве $$$S$$$ и в загаданной вершине выигрывает первый игрок.
- «Lose», если в комбинаторной игре с фишками в мультимножестве $$$S$$$ и в загаданной вершине выигрывает второй игрок.
- «Draw», если в комбинаторной игре с фишками в мультимножестве $$$S$$$ и в загаданной вершине ни один из игроков не может обеспечить себе победу.
- «Slow», если решение сделало 21-й запрос, или суммарный размер мультимножеств стал больше чем 20. В этом случае необходимо завершить выполнение, и решение будет выставлен вердикт Wrong Answer
Когда загаданная вершина определена, необходимо напечатать «! v». Если номер загаданной вершины определен правильно, интерактор в ответ напечатает Correct и надо перейти к следующей фазе отгадывания, либо завершить выполнение, если эта фаза была последней. Иначе, интерактор в ответ напечает Wrong, необходимо завершить выполнение и вашему решению будет выставлен вердикт Wrong Answer.
Интерактор имеет право менять загаданную вершину в зависимости от добавленных ребер и запросов которые делает решение, но в каждый момент в графе будет существовать хотя бы одна вершина, которая согласованна со всеми уже данными ответами.
Формат взлома
Во взломах действуют следующие дополнительные ограничения:
- $$$T = 1$$$
- Надо указать конкретную вершину, загаданную интерактором.
Формат теста для взлома — в первой строке три числа — $$$N~M~1$$$. После чего $$$M$$$ строк с ребрами, аналогично формату ввода, после чего одно число $$$v$$$ — номер загаданной вершины. Взлом будет успешным в том числе, если участник угадает вершину, но она будет не единственной, которая подходит под все сделанные участником запросы.
3 2 3 1 2 2 3 Lose Correct Win Correct Draw Correct
6 + 2 2 - 1 2 + 2 3 - 2 2 + 3 1 + 2 2 ? 0 ! 1 ? 1 2 ! 3 ? 5 1 3 1 3 1 ! 2
Пустыми строками в примерах обозначено ожидание ввода с другой стороны. В реальном вводе этих пустых строк не будет, и в выводе их быть не должно.
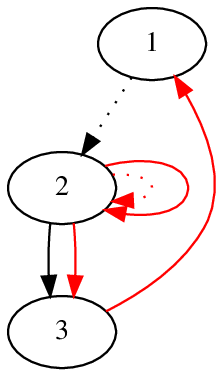
На картинке выше изображен пример. Красным обозначены добавленные ребра, пунктирным — удаленные. В трех фазах угадывания продемонстрированы разные способы, как на таком графе можно узнать ответ.
- Если не добавлять к загаданной вершине ничего, то интерактор скажет результат игры в ней. Первый игрок начиная проиграет только если загадана вершина $$$1$$$.
- Если к загаданной вершине добавить фишку в вершину $$$2$$$, то если загаданы вершины $$$1$$$ или $$$2$$$, результатом будет ничья. Если же загадана вершина $$$3$$$, то первый игрок может обеспечить себе победу.
- Если поставить три фишки в вершину $$$1$$$ и две в вершину $$$3$$$, то позиция будет ничейной, только если загадана вершина $$$2$$$. Если загадана вершина $$$3$$$, то позиция будет выигрышной для первого игрока, если вершина $$$1$$$ — проигрышной.
Обратите внимание, что при тестировании на первом тесте, интерактор будет вести себя так, как будто загаданы те же вершины, что в примере выше. Однако, если вы попытаетесь угадать ответ, когда он еще не известен однозначно, решение получит «Wrong Answer», даже если вывести те же ответы, так как интерактор имеет право поменять выбранную вершину, если это согласовано со всеми предыдущими ответами.
| Название |
|---|




