Одним осенним днём Джо заскучал от того, что не может найти себе интересное занятие. Чтобы как-то развлечь Джо, его друг Марти предложил ему сгенерировать строку длины $$$n$$$. Казалось бы, в этом нет ничего сложного, однако Джо должен был сгенерировать свою строку по следующим правилам:
- строка может содержать только символы 'a', 'b' или 'c';
- максимальная длина подстроки данной строки, которая является палиндромом, не превосходит $$$k$$$.
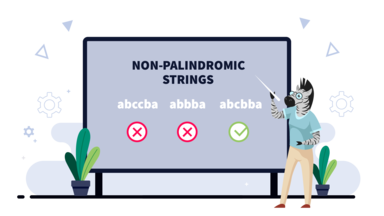
Строка $$$a$$$ является подстрокой строки $$$b$$$, если $$$a$$$ может быть получена из $$$b$$$ удалением нескольких (возможно, ни одного или всех) символов из начала и нескольких (возможно, ни одного или всех) символов из конца. Например, строки «a», «bc», «abc» являются подстроками строки «abc», а строки «ac», «ba», «cba» — нет.
Строка называется палиндромом, если она одинаково читается слева направо и справа налево. Например, строки «abccba», «abbba», «aba», «abacaba», «a» и «bacab» — палиндромы, а строки «abcbba», «abb» и «ab» — нет.
Теперь Джо интересует, как может выглядеть любая подходящая строка. Помогите ему! Можно доказать, что при заданных ограничениях ответ всегда существует.
Каждый тест содержит один или несколько наборов входных данных. В первой строке записано количество наборов входных данных $$$t$$$ ($$$1 \le t \le 10$$$).
Единственная строка каждого набора входных данных содержит два целых числа $$$n$$$ и $$$k$$$ ($$$1 \le k \le n \le 1\,000$$$) — требуемый размер строки и максимальную длину палиндромной подстроки соответственно.
Для каждого набора входных данных выведите любую строку, удовлетворяющую ограничениям из условия задачи. Если существует несколько подходящих строк, то разрешается вывести любую из них. Можно доказать, что при заданных ограничениях ответ всегда существует.
2 3 2 4 1
aab acba
В первом наборе входных данных палиндромной подстрокой с максимальной длиной является подстрока «aa». Её длина не превосходит $$$2$$$, а значит она является подходящей.
Во втором наборе входных данных все палиндромные подстроки имеют единичную длину.
| Название |
|---|




