| Codeforces Global Round 13 |
|---|
| Закончено |
Yuezheng Ling дает Luo Tianyi дерево, которое имеет $$$n$$$ вершин, с корнем $$$1$$$.
Luo Tianyi скажет вам, что непосредственным родителем вершины $$$i$$$ является $$$a_i$$$ ($$$1 \leq a_i<i$$$ для $$$2 \le i \le n$$$), и попросит вас выполнить $$$q$$$ запросов $$$2$$$ типов:
- Она даст вам три целых числа $$$l$$$, $$$r$$$ и $$$x$$$ ($$$2 \le l \le r \le n$$$, $$$1 \le x \le 10^5$$$). Вы должны заменить $$$a_i$$$ на $$$\max(a_i-x,1)$$$ для всех $$$i$$$ с $$$l \leq i \leq r$$$.
- Она даст вам два целых числа $$$u$$$, $$$v$$$ ($$$1 \le u, v \le n$$$). Вы должны найти LCA вершин $$$u$$$ и $$$v$$$ (их наименьший общий предок).
Первая строка содержит два целых числа $$$n$$$ и $$$q$$$ ($$$2\leq n,q \leq 10^5$$$) — количество вершин и количество запросов соответственно.
Вторая строка содержит $$$n-1$$$ целых чисел $$$a_2, a_3,\dots, a_n$$$ ($$$1 \le a_i < i$$$), где $$$a_i$$$ является родителем узла $$$i$$$.
Следующие $$$q$$$ строк содержат запросы. Для каждого запроса первым целым числом cтроки является $$$t$$$ ($$$t = 1$$$ или $$$2$$$) — тип запроса.
Если $$$t = 1$$$, то это запрос первого типа. Затем последуют три целых числа: $$$l$$$, $$$r$$$, $$$x$$$ ($$$2 \le l \le r \le n$$$, $$$1 \le x \le 10^5$$$), что означает, что нужно заменить $$$a_i$$$ на $$$\max(a_i-x,1)$$$ для всех $$$i$$$ с $$$l \leq i \leq r$$$. .
Если $$$t = 2$$$, то это запрос второго типа. Затем последуют два целых числа: $$$u$$$ и $$$v$$$ ($$$1 \le u, v \le n$$$), и вы должны найти LCA $$$u$$$ и $$$v$$$.
Гарантируется, что есть хотя бы один запрос второго типа.
На каждый запрос второго типа выведите ответ в новой строке.
6 4 1 2 3 3 4 2 3 4 1 2 3 1 2 5 6 2 2 3
3 3 1
Дерево в примере показано ниже.
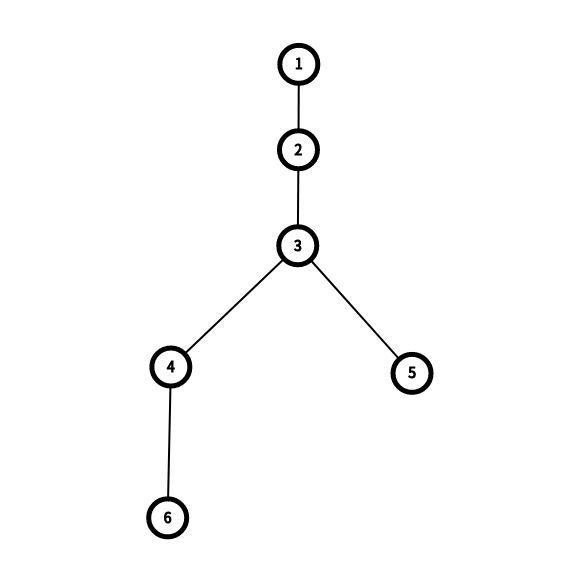
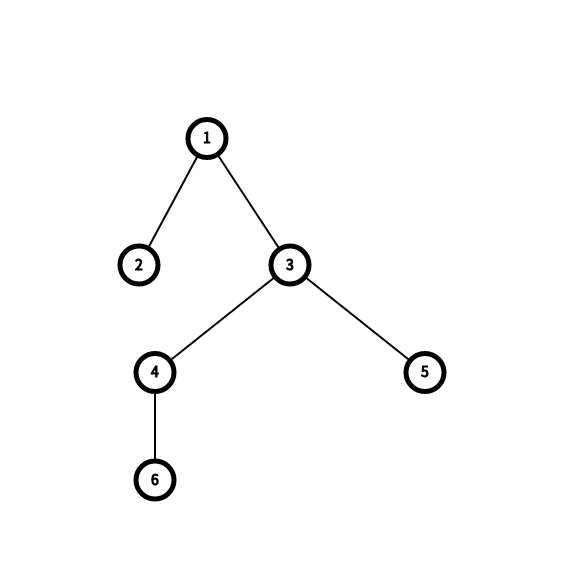
После запроса первого типа дерево становится таким, как показано ниже.
| Название |
|---|




