| Codeforces Round 707 (Div. 2, по задачам Открытой олимпиады школьников по программированию) |
|---|
| Закончено |
На этой неделе Аркадий хотел последовать традициям, испечь стопку блинов и придумать про это задачу. Однако он вспомнил, что чтобы придумать задачу про стопки блинов, нужно работать в одной известной IT-компании, поэтому вместо этого Аркадий решил испечь торт «Наполеон».
Чтобы испечь торт «Наполеон», нужно сначала выпечь $$$n$$$ сухих коржей (слоев), а затем сложить их друг на друга, пропитывая кремом. Аркадий начал с пустого блюда, и повторил следующие шаги $$$n$$$ раз:
- положил новый сухой слой на верх стопки;
- после того, как он положил $$$i$$$-й слой, он добавил на верх стопки $$$a_i$$$ ложек крема.
Когда Аркадий добавляет $$$x$$$ ложек крема на верх стопки, $$$x$$$ верхних слоев торта пропитываются кремом. Если с торте в этот момент меньше $$$x$$$ слоев, то пропитываются все эти слои, а оставшийся крем пропадает. Если $$$x = 0$$$, то не пропитывается ни один слой.
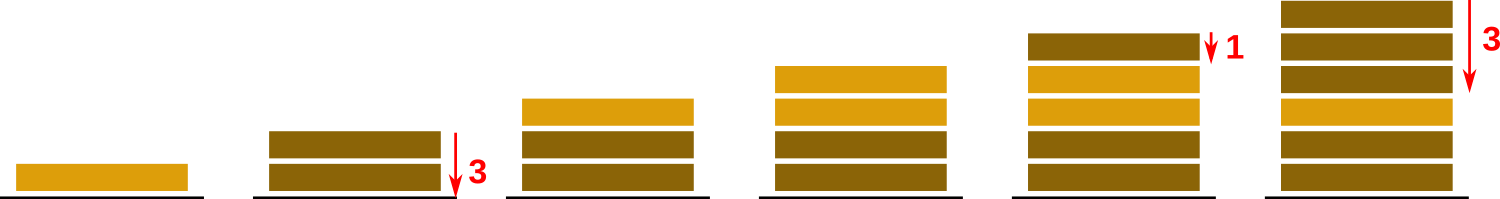 Рисунок иллюстрирует первый набор входных данных из примера.
Рисунок иллюстрирует первый набор входных данных из примера. Помогите Аркадию определить, какие слои окажутся пропитаны кремом, когда он закончит собирать торт, а какие нет.
Во входных данных находятся несколько наборов входных данных. В первой строке находится одно целое число $$$t$$$ ($$$1 \le t \le 20\,000$$$) — количество наборов входных данных. Далее следуют наборы входных данных.
Первая строка набора входных данных содержит целое число $$$n$$$ ($$$1 \le n \le 2 \cdot 10^5$$$) — количество слоев в торте.
Вторая строка каждого набора содержит $$$n$$$ целых чисел $$$a_1, a_2, \ldots, a_n$$$ ($$$0 \le a_i \le n$$$) — объем крема, добавленного после добавления каждого слоя.
Гарантируется, что сумма значений $$$n$$$ по всем наборам входных данных не превосходит $$$2 \cdot 10^5$$$.
Для каждого набора входных данных выведите одну строку с $$$n$$$ целыми числами. $$$i$$$-е из этих чисел должно быть равно $$$1$$$, если $$$i$$$-й слой снизу окажется пропитанным, и $$$0$$$ иначе.
3 6 0 3 0 0 1 3 10 0 0 0 1 0 5 0 0 0 2 3 0 0 0
1 1 0 1 1 1 0 1 1 1 1 1 0 0 1 1 0 0 0
| Название |
|---|




