| Codeforces Round 710 (Div. 3) |
|---|
| Закончено |
Рассмотрим бесконечный треугольник, состоящий из слоев. Занумеруем слои, начиная с единицы, от верхней точки треугольника (сверху вниз). На $$$k$$$-м слое треугольника расположены $$$k$$$ точек, пронумерованных слева направо. Каждая точка бесконечного треугольника описывается парой чисел $$$(r, c)$$$ ($$$1 \le c \le r$$$), где $$$r$$$ — номер слоя, а $$$c$$$ — номер точки в слое. Из каждой точки $$$(r, c)$$$ исходит два направленных ребра в точки $$$(r+1, c)$$$ и $$$(r+1, c+1)$$$, но только одно из рёбер активировано. Если $$$r + c$$$ — чётно, тогда активировано ребро в точку $$$(r+1, c)$$$, иначе активировано ребро в точку $$$(r+1, c+1)$$$. Изучите картинку для лучшего понимания.
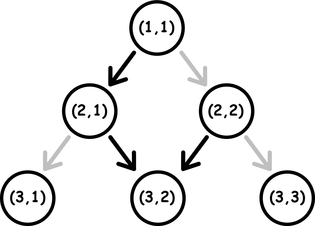Черным цветом обозначены активированные ребра. Серым цветом обозначены не активированные ребра. Из точки $$$(r_1, c_1)$$$ можно дойти до точки $$$(r_2, c_2)$$$, если между ними существует путь только из активированных рёбер. Например, на картинке выше существует путь из точки $$$(1, 1)$$$ в точку $$$(3, 2)$$$, но не существует пути из точки $$$(2, 1)$$$ в точку $$$(1, 1)$$$.
Изначально вы находитесь в точке $$$(1, 1)$$$. За каждый ход вы можете:
- Заменить активированное ребро для точки $$$(r, c)$$$. То есть, если активировано ребро в точку $$$(r+1, c)$$$, то вместо него активированным станет ребро в точку $$$(r+1, c+1)$$$, иначе, если активировано ребро в точку $$$(r+1, c+1)$$$, то вместо него активированным станет ребро в точку $$$(r+1, c)$$$. Это действие увеличивает стоимость пути на $$$1$$$;
- Переместиться из текущей точку в другую, перейдя по активированному ребру. Это действие не увеличивает стоимость пути.
Вам дана последовательность из $$$n$$$ точек бесконечного треугольника $$$(r_1, c_1), (r_2, c_2), \ldots, (r_n, c_n)$$$. Найдите путь минимальной стоимости из точки $$$(1, 1)$$$, проходящий через все $$$n$$$ точек в произвольном порядке.
Первая строка содержит одно целое $$$t$$$ ($$$1 \le t \le 10^4$$$) — количество наборов входных данных. Далее следуют $$$t$$$ наборов входных данных.
Каждый набор начинается со строки, в которой записано одно целое число $$$n$$$ ($$$1 \le n \le 2 \cdot 10^5$$$) — количество точек, которые необходимо посетить.
Во второй строке находится $$$n$$$ чисел $$$r_1, r_2, \ldots, r_n$$$ ($$$1 \le r_i \le 10^9$$$), где $$$r_i$$$ — номер слоя, в котором находится $$$i$$$-я точка.
Во третьей строке находится $$$n$$$ чисел $$$c_1, c_2, \ldots, c_n$$$ ($$$1 \le c_i \le r_i$$$), где $$$c_i$$$ — номер $$$i$$$-й точки в слое $$$r_i$$$.
Гарантируется, что все $$$n$$$ точек различны.
Гарантируется, что всегда существует хотя бы один способ обойти все $$$n$$$ точек.
Гарантируется, что сумма $$$n$$$ по всем наборам входных данных не превосходит $$$2 \cdot 10^5$$$.
Для каждого набора входных данных выведите одно целое число — минимальную стоимость пути, проходящего через все точки в соответствующем наборе входных данных.
4 3 1 4 2 1 3 1 2 2 4 2 3 2 1 1000000000 1 1000000000 4 3 10 5 8 2 5 2 4
0 1 999999999 2
