
Василий очень хочет завести себе питомца. Еще с детства он мечтал иметь домашнего кузнечика. Василий подходит к выбору питомца очень ответственно, поэтому он хочет устроить кузнечику испытание!
Испытание Василия проходит на массиве $$$a$$$ длины $$$n$$$, который задает длины прыжков для каждой из $$$n$$$ клеток. Кузнечик может прыгать по клеткам по следующим правилам: с клетки с индексом $$$i$$$ он может прыгнуть в любую клетку с индексом от $$$i$$$ до $$$i+a_i$$$ включительно.
Назовем $$$k$$$-кузнечным числом некоторого массива минимальное количество прыжков, которое потребуется кузнечику, чтобы пропрыгать от первой клетки массива до последней, при этом до начала прыжков вы можете выбрать не более $$$k$$$ клеток и удалить их из массива. Когда клетка удаляется, остальные клетки перенумеровываются, однако величина $$$a_i$$$ для каждой клетки остается неизменной. При этом нельзя удалять первую и последнюю клетки массива.
Требуется обработать $$$q$$$ запросов следующего вида: даны три числа $$$l$$$, $$$r$$$, $$$k$$$, необходимо найти $$$k$$$-кузнечное число для массива, являющегося подотрезком массива $$$a$$$ с клетками от $$$l$$$ до $$$r$$$ включительно.
Первая строка содержит два целых числа $$$n$$$ и $$$q$$$ ($$$1 \le n, q \le 20000$$$) — длину массива и количество запросов соответственно.
Вторая строка содержит $$$n$$$ целых чисел $$$a_1, a_2, \ldots, a_n$$$ ($$$1 \le a_i \le n$$$) — описание элементов массива.
Следующие $$$q$$$ строк содержат запросы: в каждой строке содержатся три целых числа $$$l$$$, $$$r$$$, $$$k$$$ ($$$1 \le l \le r \le n$$$, $$$0 \le k \le min(30, r-l)$$$) — границы подотрезков массива и номер кузнечного числа соответственно.
Для каждого запроса в отдельной строке выведите одно целое число — ответ на запрос.
9 5 1 1 2 1 3 1 2 1 1 1 1 0 2 5 1 5 9 1 2 8 2 1 9 4
0 2 1 2 2
Для второго запроса процесс происходит так: 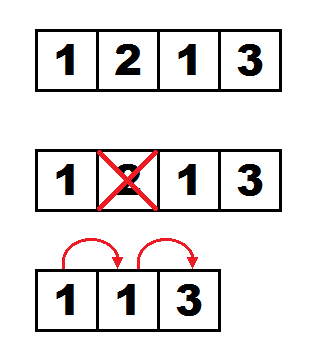
Для третьего запроса процесс происходит так: 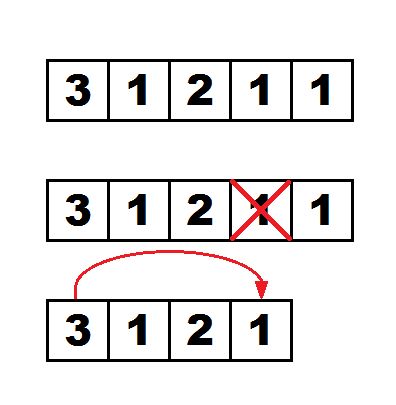
| Название |
|---|




