$$$n$$$ роботов ездят по координатной оси OX. На этой оси также есть две стены: одна в координате $$$0$$$, другая в координате $$$m$$$.
$$$i$$$-й робот начинает в целой координате $$$x_i~(0 < x_i < m)$$$ и движется либо влево (в сторону $$$0$$$), либо вправо со скоростью $$$1$$$ в секунду. Никакие два робота не начинают в одной координате.
Когда робот достигает стены, он мгновенно разворачивается и продолжает свою поездку в противоположном направлении с той же скоростью.
Когда несколько роботов встречаются в одной целой координате, они сталкиваются и взрываются. Как только робот взорвался, он больше не сталкивается с другими роботами. Обратите внимание, что если роботы встретятся в нецелой координате, то ничего не случится.
Для каждого робота проверьте, взорвется ли он когда-нибудь, и выведите время взрыва, если да, и $$$-1$$$ в противном случае.
В первой строке записано одно целое число $$$t$$$ ($$$1 \le t \le 1000$$$) — количество наборов входных данных.
Затем следуют описания $$$t$$$ наборов входных данных.
В первой строке каждого набора входных данных записаны два целых числа $$$n$$$ и $$$m$$$ ($$$1 \le n \le 3 \cdot 10^5$$$; $$$2 \le m \le 10^8$$$) — количество роботов и координата правой стены.
Во второй строке каждого набора входных данных записаны $$$n$$$ целых чисел $$$x_1, x_2, \dots, x_n$$$ ($$$0 < x_i < m$$$) — начальные координаты каждого робота.
В третьей строке каждого набора входных данных записаны $$$n$$$ символов 'L' или 'R' — начальные направления роботов ('L' означает влево, а 'R' означает вправо).
Все координаты $$$x_i$$$ в наборе входных данных различны.
Сумма $$$n$$$ по всем наборам входных данных не превосходит $$$3 \cdot 10^5$$$.
На каждый набор входных данных выведите $$$n$$$ целых чисел — для $$$i$$$-го робота выведите время взрыва, если он взорвется, и $$$-1$$$ в противном случае.
5 7 12 1 2 3 4 9 10 11 R R L L R R R 2 10 1 6 R R 2 10 1 3 L L 1 10 5 R 7 8 6 1 7 2 3 5 4 R L R L L L L
1 1 1 1 2 -1 2 -1 -1 2 2 -1 -1 2 7 3 2 7 3
Изображение секунд $$$0, 1, 2$$$ и $$$3$$$ для первого набора входных данных:
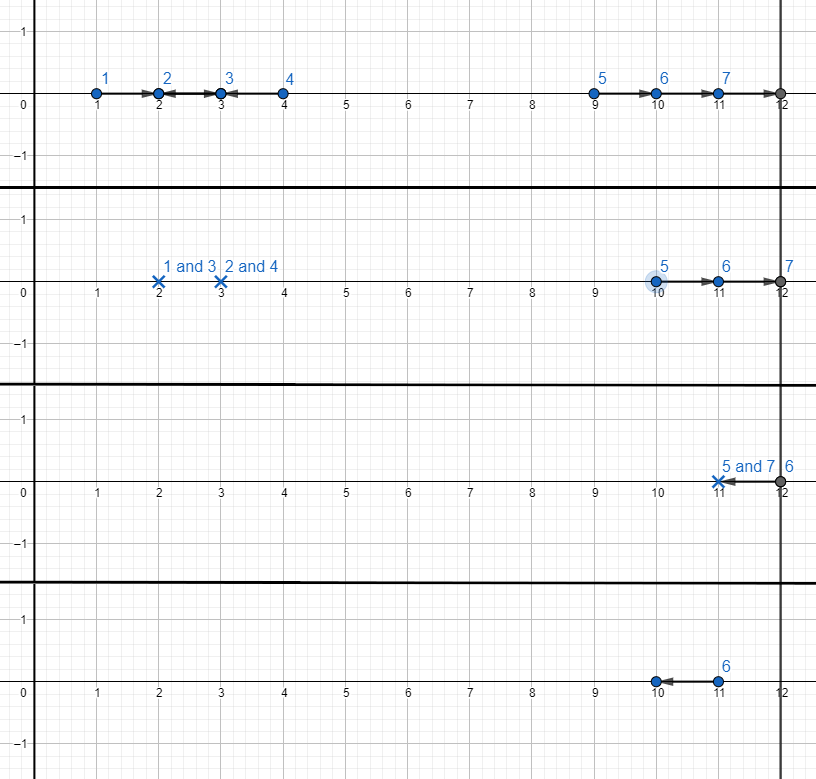
Обратите внимание, что роботы $$$2$$$ и $$$3$$$ не сталкиваются, потому что они встречаются в одной точке $$$2.5$$$, которая не является целой.
После секунды $$$3$$$ робот $$$6$$$ просто ездит бесконечно, потому что нет робота, с которым он мог бы столкнуться.
| Название |
|---|




