| Codeforces Round 722 (Div. 1) |
|---|
| Закончено |
Сегодня у Mashtali день рождения! Он получил в подарок от Haj Davood дерево Hagh!
Ориентированное дерево называется деревом Hagh, если:
- Длина самого длинного ориентированного пути в нем равна ровно $$$n$$$.
- Каждая вершина имеет не более трех ребер, присоединенных к ней (исходящих и входящих вместе).
- Назовем вершины $$$u$$$ и $$$v$$$ друзьями, если из одной из них есть ориентированный путь к другой. Для каждой пары вершин $$$u$$$ и $$$v$$$, которые не являются друзьями, должна существовать вершина $$$w$$$, которая дружит и с $$$u$$$, и с $$$v$$$ (общий друг).
Открыв свой подарок, Mashtali обнаружил, что номера вершин с вершин исчезли.
Тогда он спросил себя: сколько существует различных непомеченных деревьев Hagh? Другими словами, сколько возможных деревьев он мог получить в подарок на день рождения?
На первый взгляд, число таких деревьев кажется бесконечным, поскольку нет никакого ограничения на количество вершин; но затем он решил задачу и доказал, что непомеченых деревьев Hagh есть всего конечное число!
Пораженный этим фактом, он поделился задачей с вами, чтобы вы тоже могли насладиться ее решением. Поскольку ответ может быть довольно большим, он попросил вас найти количество различных деревьев Hagh по модулю $$$998244353$$$.
Здесь два дерева считаются различными, если они не изоморфны: если нет способа поставить в соответствие вершины одного дерева вершинам второго дерева так, чтобы ребрам первого ставились в соответствие ребра второго, с сохранением ориентации.
Некоторые примеры для $$$n = 2$$$:
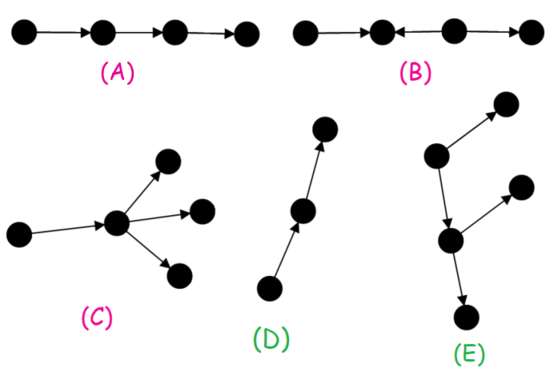
Первая строка ввода содержит единственное целое число $$$n$$$ $$$(1 \le n \le 10^6)$$$.
Выведите одно целое число, ответ на задачу Mashtali по модулю $$$998244353$$$.
1
5
2
31
344031
272040628
Вот все пять деревьев Hagh для $$$n = 1$$$:
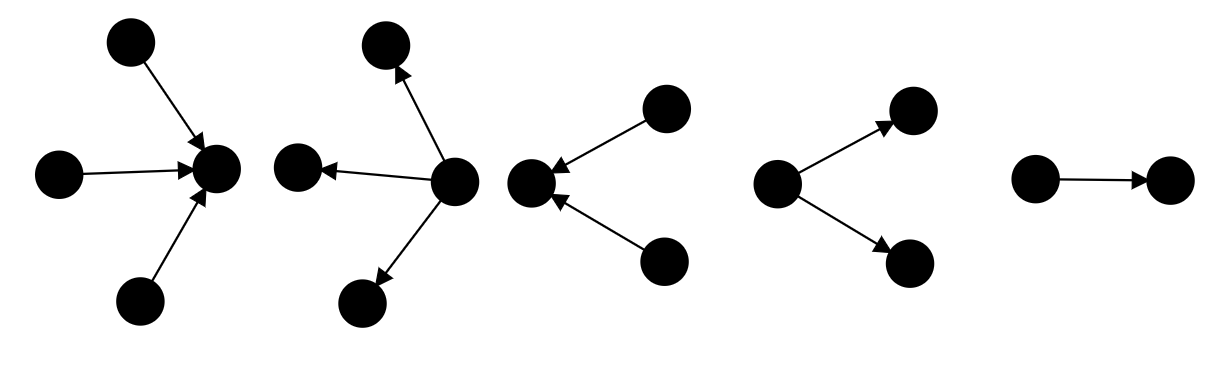
| Название |
|---|




