| Codeforces Round 722 (Div. 2) |
|---|
| Закончено |
У Kavi есть $$$2n$$$ точек, лежащих на оси $$$OX$$$, $$$i$$$-я из которых расположена в точке $$$x = i$$$.
Kavi рассматривает все способы разбить эти $$$2n$$$ точек на $$$n$$$ пар. Среди этих способов его интересуют хорошие способы, которые определяются следующим образом:
Рассмотрим $$$n$$$ отрезков с концами в точках в соответствующих парах. Пара называется хорошей, если для каждых $$$2$$$ различных отрезков $$$A$$$ и $$$B$$$ из этих, для них выполняется хотя бы одно из следующих условий:
- Один из отрезков $$$A$$$ и $$$B$$$ полностью содержится внутри другого.
- $$$A$$$ и $$$B$$$ имеют одинаковую длину.
Рассмотрим следующий пример:
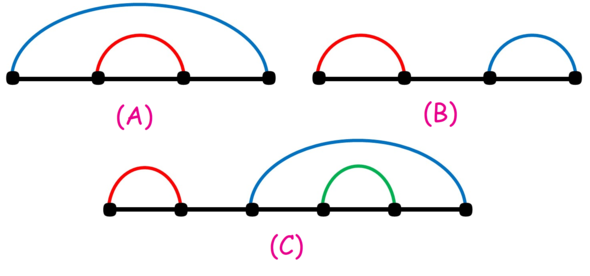
$$$A$$$ — хорошее разбиение на пары, так как красный отрезок полностью лежит внутри синего отрезка.
$$$B$$$ — хорошее разбиение, так как красный и синий отрезки имеют одинаковую длину.
$$$C$$$ не является хорошим разбиением, так как ни один из красного и синего отрезков не лежит внутри другого, и они имеют разную длину.
Kavi интересует количество хороших разбиений на пары, поэтому он хочет, чтобы вы нашли его для него. Поскольку результат может быть большим, найдите это число по модулю $$$998244353$$$.
Два разбиения на пары называются различными, если в одном из них какие-то две точки находятся в одной паре, а в другом — в разных парах.
Единственная строка ввода содержит единственное целое число $$$n$$$ $$$(1\le n \le 10^6)$$$.
Выведите количество хороших пар по модулю $$$998244353$$$.
1
1
2
3
3
6
100
688750769
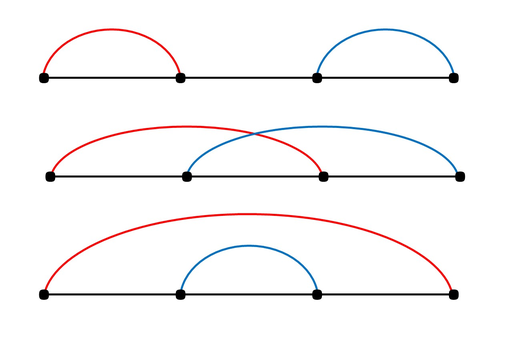
Хорошими разбиениями на пары для второго примера являются:
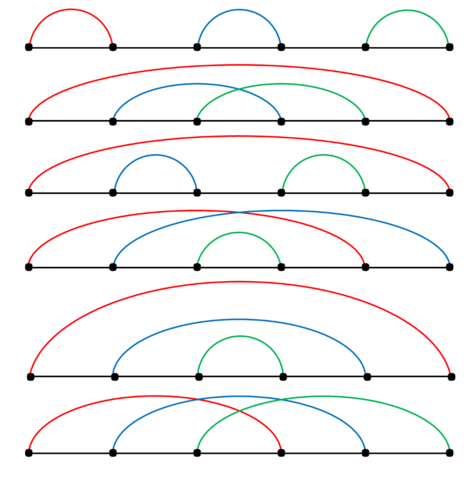
Хорошими разбиениями на пары для третьего примера являются:
| Название |
|---|




