Это интерактивная задача.
Маленький Дорми на фестивале столкнулся со странной головоломкой: ему нужно угадать ребра невзвешенного дерева из $$$n$$$ вершин! Вершины дерева пронумерованы от $$$1$$$ до $$$n$$$.
Ему разрешается задавать организатору вопросы одного вида:
- Маленький Дорми выбирает вершину $$$r$$$ ($$$1 \le r \le n$$$), а организатор в ответ предоставляет ему массив целых чисел $$$d_1, d_2, \ldots, d_n$$$, где $$$d_i$$$ — длина кратчайшего пути из $$$r$$$ в вершину $$$i$$$ для всех $$$1 \le i \le n$$$.
Кроме того, чтобы сделать головоломку нечестной дополнительно озадачить Дорми, организатор разрешает задать не более $$$\lceil\frac{n}{2}\rceil$$$ вопросов, где $$$\lceil x \rceil$$$ обозначает наименьшее целое число, большее либо равное $$$x$$$.
Маленький Дорми переживает, что может не угадать дерево, поэтому ему нужна ваша помощь!
Обратите внимание, что организатор создает дерево до начала взаимодействия, и не меняет его в процессе взаимодействия.
Первая строка содержит одно целое число $$$n$$$ ($$$2 \le n \le 2\,000$$$) — количество вершин в дереве.
После этого начинается взаимодействие.
Когда ваша программа нашла дерево, выведите одну строку, содержащую «!», а затем $$$n-1$$$ строку, каждая из которых содержит два целых числа $$$a$$$ и $$$b$$$, означающие ребро, соединяющее вершины $$$a$$$ и $$$b$$$ ($$$1 \le a, b \le n$$$). После этого ваша программа должна сбросить буфер вывода и завершиться.
Вы можете выводить ребра дерева в любом порядке, ребро $$$(a,b)$$$ и ребро $$$(b,a)$$$ считаются одним и тем же ребром. Вывод ответа не считается как один из вопросов.
После чтения количества вершин, вы можете задать не более $$$\lceil\frac{n}{2}\rceil$$$ вопросов. Каждый вопрос задается в формате «? r», где целое число $$$r$$$ ($$$1 \le r \le n$$$) обозначает номер вершины, которую вы выбрали для этого вопроса.
После этого считайте $$$n$$$ целых чисел $$$d_1, d_2, \ldots, d_n$$$ в отдельной строке, где $$$d_i$$$ равно длине кратчайшего пути из вершины $$$r$$$ в вершину $$$i$$$.
После вывода запроса не забудьте вывести перевод строки и сбросить буфер вывода. В противном случае вы получите вердикт Решение «зависло». Для сброса буфера используйте:
- fflush(stdout) или cout.flush() в C++;
- System.out.flush() в Java;
- flush(output) в Pascal;
- stdout.flush() в Python;
- смотрите документацию для других языков.
Если в какой-то момент вы задали больше, чем $$$\lceil \frac{n}{2} \rceil$$$ вопросов, взаимодействие прекратится, и вы получите вердикт «Неправильный ответ».
Взломы
Чтобы взломать решение, используйте следующий формат теста.
Первая строка содержит целое число $$$n$$$ ($$$2 \le n \le 2\,000$$$).
Следующие $$$n−1$$$ строк содержат два целых числа $$$u$$$ и $$$v$$$ ($$$1 \le u,v \le n$$$), обозначающие ребро между вершинами $$$u$$$ и $$$v$$$ ($$$u \neq v$$$). Эти $$$n-1$$$ ребер должны образовывать дерево.
4 0 1 2 2 1 0 1 1
? 1 ? 2 ! 4 2 1 2 2 3
5 2 2 1 1 0
? 5 ! 4 5 3 5 2 4 1 3
Ниже показано дерево из первого примера.
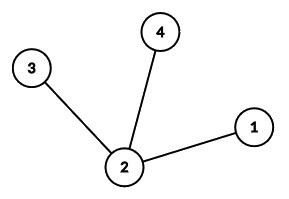
Обратите внимание, что ребра можно выводить в любом порядке.
Кроме того, ниже показаны ответы для всех возможных вопросов в примере $$$1$$$:
- $$$1$$$: $$$[0,1,2,2]$$$
- $$$2$$$: $$$[1,0,1,1]$$$
- $$$3$$$: $$$[2,1,0,2]$$$
- $$$4$$$: $$$[2,1,2,0]$$$
Ниже показано дерево из второго примера.
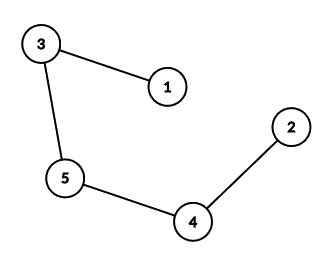
Далее показаны ответы для всех возможных вопросов в примере $$$2$$$:
- $$$1$$$: $$$[0,4,1,3,2]$$$
- $$$2$$$: $$$[4,0,3,1,2]$$$
- $$$3$$$: $$$[1,3,0,2,1]$$$
- $$$4$$$: $$$[3,1,2,0,1]$$$
- $$$5$$$: $$$[2,2,1,1,0]$$$
| Название |
|---|




