
Василий увлекается не только трейдингом, но и ставками на спортивные матчи. В матче участвует $$$n$$$ спортивных команд. Каждая команда характеризуется силой $$$a_i$$$. Каждые две команды $$$i < j$$$ играют друг с другом ровно один раз. С вероятностью $$$\frac{a_i}{a_i + a_j}$$$ побеждает команда $$$i$$$, с вероятностью $$$\frac{a_j}{a_i + a_j}$$$ побеждает команда $$$j$$$.
Команда называется победителем, если она прямо или косвенно победила все остальные команды. Команда $$$a$$$ победила (прямо или косвенно) команду $$$b$$$, если существует последовательность команд $$$c_1$$$, $$$c_2$$$, ... $$$c_k$$$ такая, что $$$c_1 = a$$$, $$$c_k = b$$$ и команда $$$c_i$$$ выиграла матч у команды $$$c_{i + 1}$$$ для всех $$$i$$$ от $$$1$$$ до $$$k - 1$$$. Обратите внимание, что возможно, что команда $$$a$$$ победила команду $$$b$$$, и в то же время команда $$$b$$$ победила команду $$$a$$$.
Василий хочет, чтобы вы помогли ему определить математическое ожидание количества победителей.
В первой строке находится целое число $$$n$$$ ($$$1 \leq n \leq 14$$$) — количество команд, участвующих в матче.
В следующей строке находится $$$n$$$ целых чисел $$$a_1, a_2, \dots, a_n$$$ ($$$1 \leq a_i \leq 10^6$$$) — силы команд, участвующих в матче.
Выведите единственное целое число — математическое ожидание количества победителей турнира по модулю $$$10^9 + 7$$$.
Формально, пусть $$$M = 10^9+7$$$. Можно показать, что ответ может быть представлен в виде несократимой дроби $$$\frac{p}{q}$$$, где $$$p$$$ и $$$q$$$ — целые числа, и $$$q \not \equiv 0 \pmod{M}$$$. Выведите целое число, равное $$$p \cdot q^{-1} \bmod M$$$. Другими словами, выведите такое целое число $$$x$$$, что $$$0 \le x < M$$$ и $$$x \cdot q \equiv p \pmod{M}$$$.
2 1 2
1
5 1 5 2 11 14
642377629
Чтобы лучше понять, в каких ситуациях возможно несколько победителей, рассмотрим второй тест:
Одним из возможных результатов сыгранных матчей является следующий ($$$a \rightarrow b$$$ означает, что $$$a$$$ выиграла матч у $$$b$$$):
- $$$1 \rightarrow 2$$$
- $$$2 \rightarrow 3$$$
- $$$3 \rightarrow 1$$$
- $$$1 \rightarrow 4$$$
- $$$1 \rightarrow 5$$$
- $$$2 \rightarrow 4$$$
- $$$2 \rightarrow 5$$$
- $$$3 \rightarrow 4$$$
- $$$3 \rightarrow 5$$$
- $$$4 \rightarrow 5$$$
Или более наглядно на рисунке:
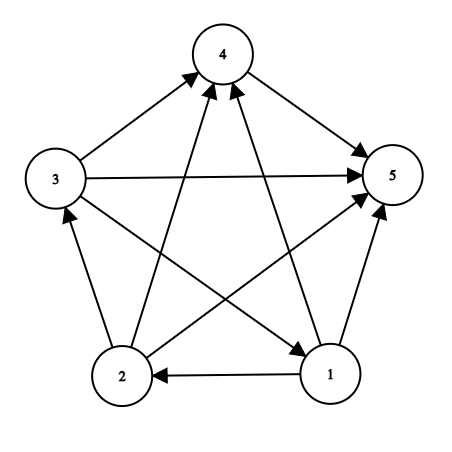
В данном варианте каждая команда из множества $$$\{ 1, 2, 3 \}$$$ прямо или косвенно победила всех. То есть:
- $$$1$$$-я победила всех, так как до остальных можно добраться следующим образом $$$1 \rightarrow 2$$$, $$$1 \rightarrow 2 \rightarrow 3$$$, $$$1 \rightarrow 4$$$, $$$1 \rightarrow 5$$$.
- $$$2$$$-я победила всех, так как до остальных можно добраться следующим образом $$$2 \rightarrow 3$$$, $$$2 \rightarrow 3 \rightarrow 1$$$, $$$2 \rightarrow 4$$$, $$$2 \rightarrow 5$$$.
- $$$3$$$-я победила всех, так как до остальных можно добраться следующим образом $$$3 \rightarrow 1$$$, $$$3 \rightarrow 1 \rightarrow 2$$$, $$$3 \rightarrow 4$$$, $$$3 \rightarrow 5$$$.
Следовательно, количество победителей равно $$$3$$$.
| Название |
|---|




