Есть город, который можно представить как квадрат на плоскости с концами в координатах $$$(0, 0)$$$ и $$$(10^6, 10^6)$$$.
В городе есть $$$n$$$ вертикальных и $$$m$$$ горизонтальных улиц, которые пересекают весь город, т. е. $$$i$$$-я вертикальная улица проходит от $$$(x_i, 0)$$$ до $$$(x_i, 10^6)$$$, а $$$j$$$-я горизонтальная улица проходит от $$$(0, y_j)$$$ до $$$(10^6, y_j)$$$.
Все улицы двухсторонние. Границы города также являются улицами.
В городе на некоторых улицах стоят $$$k$$$ человек: $$$p$$$-й человек стоит в точке $$$(x_p, y_p)$$$ (таким образом, либо $$$x_p$$$ равняется некоторому $$$x_i$$$, либо $$$y_p$$$ равняется некоторому $$$y_j$$$, либо и то и другое).
Назовем пару человек неудачной парой, если кратчайший путь от одного человека до другого, если двигаться только по улицам, строго больше чем Манхеттенское расстояние между ними.
Посчитайте общее количество неудачных пар (пары $$$(x, y)$$$ и $$$(y, x)$$$ — это одна и та же пара).
Напомним, что Манхеттенское расстояние между точками $$$(x_1, y_1)$$$ и $$$(x_2, y_2)$$$ равно $$$|x_1 - x_2| + |y_1 - y_2|$$$.
В первой строке задано одно целое число $$$t$$$ ($$$1 \le t \le 1000$$$) — количество наборов входных данных.
В первой строке каждого набора заданы три целых числа $$$n$$$, $$$m$$$ и $$$k$$$ ($$$2 \le n, m \le 2 \cdot 10^5$$$; $$$2 \le k \le 3 \cdot 10^5$$$) — количество вертикальных и горизонтальных улиц и количество человек.
Во второй строке каждого набора заданы $$$n$$$ целых чисел $$$x_1, x_2, \dots, x_n$$$ ($$$0 = x_1 < x_2 < \dots < x_{n - 1} < x_n = 10^6$$$) — $$$x$$$-координаты вертикальных улиц.
В третьей строке заданы $$$m$$$ целых чисел $$$y_1, y_2, \dots, y_m$$$ ($$$0 = y_1 < y_2 < \dots < y_{m - 1} < y_m = 10^6$$$) — $$$y$$$-координаты горизонтальных улиц.
В следующих $$$k$$$ строках заданы описания людей. В $$$p$$$-й строке заданы два целых числа $$$x_p$$$ и $$$y_p$$$ ($$$0 \le x_p, y_p \le 10^6$$$; $$$x_p \in \{x_1, \dots, x_n\}$$$ или $$$y_p \in \{y_1, \dots, y_m\}$$$) — координаты $$$p$$$-го человека. Все координаты различны.
Гарантируется, что сумма $$$n$$$ не превосходит $$$2 \cdot 10^5$$$, сумма $$$m$$$ не превосходит $$$2 \cdot 10^5$$$ и сумма $$$k$$$ не превосходит $$$3 \cdot 10^5$$$.
Для каждого набора входных данных, выведите общее количество неудачных пар людей.
2 2 2 4 0 1000000 0 1000000 1 0 1000000 1 999999 1000000 0 999999 5 4 9 0 1 2 6 1000000 0 4 8 1000000 4 4 2 5 2 2 6 3 1000000 1 3 8 5 8 8 8 6 8
2 5
Изображение второго набора входных данных представлено ниже:
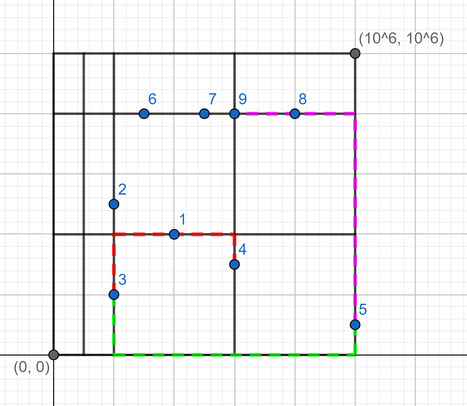
Для примера, точки $$$3$$$ и $$$4$$$ образуют неудачную пару, потому что кратчайший путь между ними (отмечен красным и равен $$$7$$$) больше, чем их Манхеттенское расстояние (равное $$$5$$$).
Точки $$$3$$$ и $$$5$$$ также образуют неудачную пару: кратчайший путь равен $$$1000001$$$ (отмечен зеленым) больше, чем Манхеттенское расстояние равное $$$999999$$$.
Однако, точки $$$5$$$ и $$$9$$$ не образуют неудачную пару, потому что кратчайший путь (отмечен фиолетовым) равен их Манхеттенскому расстоянию.
| Название |
|---|




