| Hello 2022 |
|---|
| Закончено |
У Вас есть квадратная клетчатая доска $$$n \times n$$$ и $$$k$$$ ладей. Строки этой доски пронумерованы числами от $$$1$$$ до $$$n$$$ сверху вниз, а столбцы пронумерованы числами от $$$1$$$ до $$$n$$$ слева направо. Клетка $$$(x, y)$$$ — это клетка на пересечении строки $$$x$$$ и столбца $$$y$$$ для $$$1 \leq x \leq n$$$ и $$$1 \leq y \leq n$$$.
Назовём расстановку ладей на эту доску хорошей, если никакая ладья не находится под боем другой ладьи.
Напомним, что ладья бьёт всех ладей, которые находятся с ней в одной строке или в одном столбце.
Назовём хорошую расстановку ладей на эту доску устойчивой, если не существует способа передвинуть одну из ладей на одну из соседних по стороне клеток, чтобы расстановка ладей перестала быть хорошей.
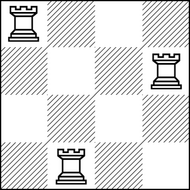Такая расстановка $$$3$$$ ладей на доске $$$4 \times 4$$$ является хорошей, но не является устойчивой: ладью с клетки $$$(1, 1)$$$ можно подвинуть на клетку $$$(2, 1)$$$ и после этого ладьи на клетках $$$(2, 1)$$$ и $$$(2, 4)$$$ будут бить друг друга. Найдите любую устойчивую расстановку $$$k$$$ ладей на доске $$$n \times n$$$ или сообщите, что такой расстановки не существует.
В первой строке задано одно целое число $$$t$$$ ($$$1 \leq t \leq 100$$$) — количество наборов входных данных. Далее следуют описания этих наборов.
В первой строке дано два числа $$$n$$$, $$$k$$$ ($$$1 \leq k \leq n \leq 40$$$) — длина стороны доски и количество ладей.
Если устойчивая расстановка $$$k$$$ ладей на доске $$$n \times n$$$ существует, выведите $$$n$$$ строк из символов . и R. $$$j$$$-й символ $$$i$$$-й строки должен быть равен R тогда и только тогда, когда в вашей расстановке есть ладья в клетке $$$(i, j)$$$.
Если существует несколько решений, Вы можете вывести любое из них.
Если устойчивой расстановки ладей не существует, выведите $$$-1$$$.
53 23 31 15 240 33
..R ... R.. -1 R ..... R.... ..... ....R ..... -1
В первом наборе входных данных Вам надо найти устойчивую расстановку $$$2$$$ ладей на доске $$$3 \times 3$$$. Постановка их в клетки $$$(3, 1)$$$ и $$$(1, 3)$$$ даёт устойчивую расстановку.
Во втором наборе входных данных можно показать, что нельзя расставить $$$3$$$ ладьи на доске $$$3 \times 3$$$ и получить устойчивую расстановку.
