На горе, покрытой снегом, $$$n$$$ отмеченных площадок, пронумерованных от $$$1$$$ до $$$n$$$, соединенных $$$n-1$$$ трассой в форме дерева. Каждая трасса имеет длину $$$1$$$. Некоторые из площадок являются базами. Высота $$$h_i$$$ каждой площадки равна расстоянию до ближайшей базы (все базы имеют высоту $$$0$$$).
На каждой площадке находится по одному лыжнику, изначально кинетическая энергия каждого лыжника равна $$$0$$$. Каждый лыжник хочет съехать по наибольшему количеству трасс. Предположим, что лыжник едет по трассе от $$$i$$$-й площадки до $$$j$$$-й. Лыжники не могут двигаться вверх (т. е. невозможно, что $$$h_i < h_j$$$). При проезде горизонтального участка (т. е. если $$$h_i = h_j$$$) лыжник теряет одну единицу кинетической энергии, а при спуске (т. е. если $$$h_i > h_j$$$) лыжник получает одну единицу кинетической энергии. Для каждой площадки определите длину наибольшей последовательность трасс, начинающуюся с данной площадки, которую может проехать лыжник, не уменьшая свою кинетическую энергию ниже нуля. Лыжники могут посещать одну и ту же площадку и проезжать одну и ту же трассу несколько раз.
Первая строка содержит одно целое число $$$n$$$ ($$$2 \le n \le 2 \cdot 10^5$$$).
Вторая строка содержит $$$n$$$ целых чисел $$$l_1, l_2, \ldots, l_n$$$ ($$$0 \le l_i \le 1$$$). Если $$$l_i = 1$$$, площадка $$$i$$$ является базой; если $$$l_i = 0$$$, площадка $$$i$$$ не является базой. Гарантируется, что есть хотя бы $$$1$$$ база.
Каждая из следующих $$$n-1$$$ строк содержит два целых числа $$$u, v$$$ ($$$1 \leq u, v \leq n$$$, $$$u \neq v$$$), означающих, что есть трасса, соединяющая площадки $$$u$$$ и $$$v$$$. Гарантируется, что данные трассы образуют дерево.
Выведите $$$n$$$ целых чисел: $$$i$$$-е число должно быть равно длине наибольшей последовательности трасс, которую может проехать лыжник, начав на площадке $$$i$$$, не уменьшая кинетическую энергию ниже нуля.
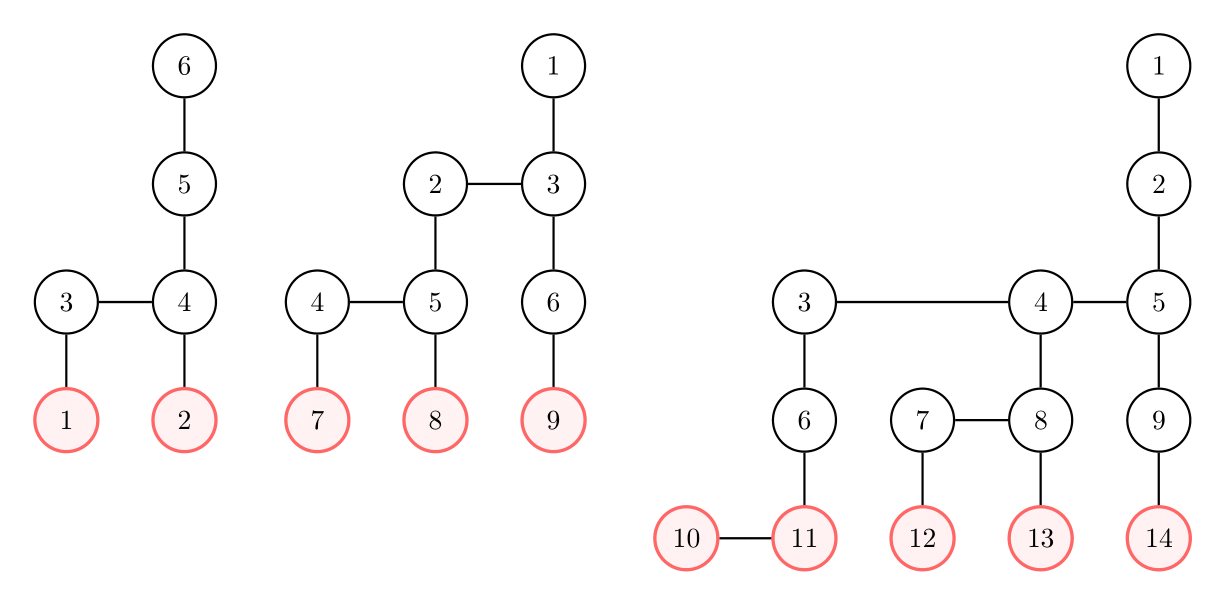
6 1 1 0 0 0 0 1 3 2 4 3 4 4 5 5 6
0 0 1 1 3 5
9 0 0 0 0 0 0 1 1 1 1 3 2 3 2 5 3 6 4 5 4 7 5 8 6 9
5 3 2 1 1 1 0 0 0
14 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 2 2 5 3 4 4 5 3 6 4 8 5 9 7 8 6 11 7 12 8 13 9 14 10 11
8 5 4 3 2 2 1 1 1 0 0 0 0 0
20 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 0 1 0 1 17 3 11 12 6 10 18 19 8 14 16 20 5 3 2 11 7 10 2 15 8 3 3 15 9 16 7 13 16 1 19 2 2 16 6 1 4 17
2 2 1 5 3 4 8 1 2 6 4 6 10 0 0 0 3 0 1 0
В первом примере $$$h = [0, 0, 1, 1, 2, 3]$$$. Лыжник, начинающий на площадке $$$6$$$ может проехать максимум $$$5$$$ трасс по пути $$$6 \rightarrow 5 \rightarrow 4 \rightarrow 3 \rightarrow 4 \rightarrow 2$$$ (обратите внимание, что лыжник может посещать одну и ту же площадку и проезжать одну и ту же трассу несколько раз):
- на площадке $$$6$$$ кинетическая энергия равна $$$0$$$;
- на площадке $$$5$$$ кинетическая энергия увеличивается на $$$1$$$ (т. к. $$$h_5 < h_6$$$) и становится равной $$$1$$$;
- на площадке $$$4$$$ кинетическая энергия увеличивается на $$$1$$$ (т. к. $$$h_4 < h_5$$$) и становится равной $$$2$$$;
- на площадке $$$3$$$ кинетическая энергия уменьшается на $$$1$$$ (т. к. $$$h_3 = h_4$$$) и становится равной $$$1$$$;
- на площадке $$$4$$$ кинетическая энергия уменьшается на $$$1$$$ (т. к. $$$h_4 = h_3$$$) и становится равной $$$0$$$;
- на площадке $$$2$$$ кинетическая энергия увеличивается на $$$1$$$ (т. к. $$$h_2 < h_4$$$) и становится равной $$$1$$$.
Нет последовательности трасс длиной большей чем $$$5$$$, на которой кинетическая энергия не становилась бы отрицательной.
Далее,
- оптимальный маршрут для лыжника, стартующего с площадки $$$1$$$ — это $$$1$$$ (ноль трасс);
- оптимальный маршрут для лыжника, стартующего с площадки $$$2$$$ — это $$$2$$$ (ноль трасс);
- оптимальный маршрут для лыжника, стартующего с площадки $$$3$$$ — это $$$3 \rightarrow 1$$$;
- оптимальный маршрут для лыжника, стартующего с площадки $$$4$$$ — это $$$4 \rightarrow 2$$$;
- оптимальный маршрут для лыжника, стартующего с площадки $$$5$$$ — это $$$5 \rightarrow 4 \rightarrow 3 \rightarrow 1$$$.
Во втором примере $$$h = [3, 2, 2, 1, 1, 1, 0, 0, 0]$$$. Лыжник, начинающий на площадке $$$1$$$ может проехать максимум $$$5$$$ трасс по пути $$$1 \rightarrow 3 \rightarrow 2 \rightarrow 5 \rightarrow 4 \rightarrow 7$$$.
- на площадке $$$1$$$ кинетическая энергия равна $$$0$$$;
- на площадке $$$3$$$ кинетическая энергия увеличивается на $$$1$$$ (т. к. $$$h_3 < h_1$$$) и становится равной $$$1$$$;
- на площадке $$$2$$$ кинетическая энергия уменьшается на $$$1$$$ (т. к. $$$h_2 = h_3$$$) и становится равной $$$0$$$;
- на площадке $$$5$$$ кинетическая энергия увеличивается на $$$1$$$ (т. к. $$$h_5 < h_2$$$) и становится равной $$$1$$$;
- на площадке $$$4$$$ кинетическая энергия уменьшается на $$$1$$$ (т. к. $$$h_4 = h_5$$$) и становится равной $$$0$$$;
- на площадке $$$7$$$ кинетическая энергия увеличивается на $$$1$$$ (т. к. $$$h_7 < h_4$$$) и становится равной $$$1$$$.
Нет последовательности трасс длиной большей чем $$$5$$$, на которой кинетическая энергия не становилась бы отрицательной.
В третьем примере оптимальный маршрут для лыжника, начинающего на площадке $$$1$$$, такой: $$$1 \rightarrow 2 \rightarrow 5 \rightarrow 4 \rightarrow 3 \rightarrow 6 \rightarrow 11 \rightarrow 10 \rightarrow 11$$$.
Ниже изображены первые три примера, базы отмечены красным:
| Название |
|---|




