Bethany would like to tile her bathroom. The bathroom has width $$$w$$$ centimeters and length $$$l$$$ centimeters. If Bethany simply used the basic tiles of size $$$1 \times 1$$$ centimeters, she would use $$$w \cdot l$$$ of them.
However, she has something different in mind.
- On the interior of the floor she wants to use the $$$1 \times 1$$$ tiles. She needs exactly $$$(w-2) \cdot (l-2)$$$ of these.
- On the floor boundary she wants to use tiles of size $$$1 \times a$$$ for some positive integer $$$a$$$. The tiles can also be rotated by $$$90$$$ degrees.
For which values of $$$a$$$ can Bethany tile the bathroom floor as described? Note that $$$a$$$ can also be $$$1$$$.
Each test contains multiple test cases. The first line contains an integer $$$t$$$ ($$$1\le t\le 100$$$) — the number of test cases. The descriptions of the $$$t$$$ test cases follow.
Each test case consist of a single line, which contains two integers $$$w$$$, $$$l$$$ ($$$3 \leq w, l \leq 10^{9}$$$) — the dimensions of the bathroom.
For each test case, print an integer $$$k$$$ ($$$0\le k$$$) — the number of valid values of $$$a$$$ for the given test case — followed by $$$k$$$ integers $$$a_1, a_2,\dots, a_k$$$ ($$$1\le a_i$$$) — the valid values of $$$a$$$. The values $$$a_1, a_2, \dots, a_k$$$ have to be sorted from smallest to largest.
It is guaranteed that under the problem constraints, the output contains at most $$$200\,000$$$ integers.
33 512 12314159265 358979323
3 1 2 3 3 1 2 11 2 1 2
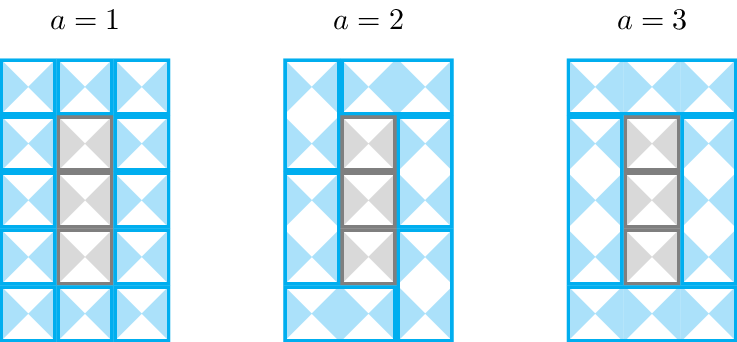
In the first test case, the bathroom is $$$3$$$ centimeters wide and $$$5$$$ centimeters long. There are three values of $$$a$$$ such that Bethany can tile the floor as described in the statement, namely $$$a=1$$$, $$$a=2$$$ and $$$a=3$$$. The three tilings are represented in the following pictures.
| Название |
|---|




