| 2021-2022 ICPC, NERC, Northern Eurasia Onsite (Unrated, Online Mirror, ICPC Rules, Teams Preferred) |
|---|
| Finished |
Julia's $$$n$$$ friends want to organize a startup in a new country they moved to. They assigned each other numbers from 1 to $$$n$$$ according to the jobs they have, from the most front-end tasks to the most back-end ones. They also estimated a matrix $$$c$$$, where $$$c_{ij} = c_{ji}$$$ is the average number of messages per month between people doing jobs $$$i$$$ and $$$j$$$.
Now they want to make a hierarchy tree. It will be a binary tree with each node containing one member of the team. Some member will be selected as a leader of the team and will be contained in the root node. In order for the leader to be able to easily reach any subordinate, for each node $$$v$$$ of the tree, the following should apply: all members in its left subtree must have smaller numbers than $$$v$$$, and all members in its right subtree must have larger numbers than $$$v$$$.
After the hierarchy tree is settled, people doing jobs $$$i$$$ and $$$j$$$ will be communicating via the shortest path in the tree between their nodes. Let's denote the length of this path as $$$d_{ij}$$$. Thus, the cost of their communication is $$$c_{ij} \cdot d_{ij}$$$.
Your task is to find a hierarchy tree that minimizes the total cost of communication over all pairs: $$$\sum_{1 \le i < j \le n} c_{ij} \cdot d_{ij}$$$.
The first line contains an integer $$$n$$$ ($$$1 \le n \le 200$$$) – the number of team members organizing a startup.
The next $$$n$$$ lines contain $$$n$$$ integers each, $$$j$$$-th number in $$$i$$$-th line is $$$c_{ij}$$$ — the estimated number of messages per month between team members $$$i$$$ and $$$j$$$ ($$$0 \le c_{ij} \le 10^9; c_{ij} = c_{ji}; c_{ii} = 0$$$).
Output a description of a hierarchy tree that minimizes the total cost of communication. To do so, for each team member from 1 to $$$n$$$ output the number of the member in its parent node, or 0 for the leader. If there are many optimal trees, output a description of any one of them.
4 0 566 1 0 566 0 239 30 1 239 0 1 0 30 1 0
2 4 2 0
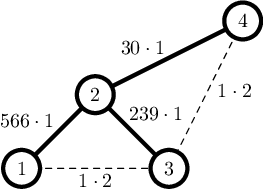
The minimal possible total cost is $$$566 \cdot 1+239 \cdot 1+30 \cdot 1+1 \cdot 2+1 \cdot 2=839$$$:
| Name |
|---|




