| Codeforces Round 802 (Div. 2) |
|---|
| Закончено |
Дана таблица $$$a$$$ размера $$$n \times m$$$. Будем считать, что строки таблицы пронумерованы сверху вниз от $$$1$$$ до $$$n$$$, а столбцы — слева направо от $$$1$$$ до $$$m$$$. Тогда клетку, находящуюся в строке $$$i$$$ и столбце $$$j$$$, будем обозначать $$$(i, j)$$$. В клетке $$$(i, j)$$$ записано число $$$(i - 1) \cdot m + j$$$, то есть $$$a_{ij} = (i - 1) \cdot m + j$$$.
Черепашка изначально находится в клетке $$$(1, 1)$$$ и хочет попасть в клетку $$$(n, m)$$$. За один шаг из клетки $$$(i, j)$$$ она может попасть в клетку $$$(i + 1, j)$$$ или $$$(i, j + 1)$$$, если она существует. Путь — это набор клеток, такой что для двух соседних клеток в пути верно следующее: из первой клетки можно попасть во вторую за один шаг. Стоимостью пути называется сумма чисел, записанных в клетках пути.
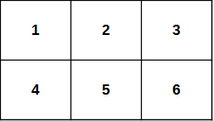
Например, при $$$n = 2$$$ и $$$m = 3$$$ таблица будет выглядеть как на картинке выше. Черепашка может пройти по такому пути: $$$(1, 1) \rightarrow (1, 2) \rightarrow (1, 3) \rightarrow (2, 3)$$$. Стоимость такого пути будет равна $$$a_{11} + a_{12} + a_{13} + a_{23} = 12$$$. С другой стороны, пути $$$(1, 1) \rightarrow (1, 2) \rightarrow (2, 2) \rightarrow (2, 1)$$$ и $$$(1, 1) \rightarrow (1, 3)$$$ являются некорректными, так как в первом случае нельзя сделать переход $$$(2, 2) \rightarrow (2, 1)$$$, а во втором случае $$$(1, 1) \rightarrow (1, 3)$$$.
Вам нужно сказать черепашке минимальную стоимость пути из клетки $$$(1, 1)$$$ в клетку $$$(n, m)$$$. Обратите внимание, что клетки $$$(1, 1)$$$ и $$$(n, m)$$$ являются частью пути.
Первая строка содержит одно целое число $$$t$$$ ($$$1 \leq t \leq 1000$$$) — количество наборов входных данных. Далее следует описание наборов входных данных.
Единственная строка каждого набора входных данных содержит два целых числа $$$n$$$ и $$$m$$$ ($$$1 \leq n, m \leq 10^4$$$) — размеры таблицы $$$a$$$.
Для каждого набора входных данных выведите одно число — минимальную стоимость пути из клетки $$$(1, 1)$$$ в клетку $$$(n, m)$$$.
71 12 33 27 11 105 510000 10000
1 12 13 28 55 85 500099995000
В первом наборе входных данных единственный возможный путь проходит только по клетке $$$(1, 1)$$$.
Путь минимальной стоимости из второго набора выходных данных показан в условии.
В четвертом и пятом наборах входных данных существует единственный путь из $$$(1, 1)$$$ в $$$(n, m)$$$. Оба пути проходят по всем клеткам таблицы.
| Название |
|---|




