Дано дерево на $$$n$$$ вершинах, корень дерева — вершина $$$1$$$. В каждой вершине написано значение, изначально (в момент $$$t=0$$$) равное $$$0$$$ или $$$1$$$.
В каждый целочисленный момент времени $$$t>0$$$ значение вершины становится равно побитовому исключающему ИЛИ значений ее детей в момент времени $$$t - 1$$$; значения листьев становятся равными $$$0$$$, поскольку у них детей нет.
Через $$$S(t)$$$ обозначим сумму значений всех вершин в момент $$$t$$$.
Через $$$F(A)$$$ обозначим сумму $$$S(t)$$$ по всем значениям $$$t$$$ в диапазоне $$$0 \le t \le 10^{100}$$$, где $$$A$$$ — некоторая изначальная расстановка $$$0$$$ и $$$1$$$ в дереве.
Ваша задача — найти сумму $$$F(A)$$$ по всем $$$2^n$$$ изначальным расстановкам $$$0$$$ и $$$1$$$ в дереве. Выведите ответ по модулю $$$10^9+7$$$.
Каждый тест состоит из нескольких наборов входных данных. В первой строке находится одно целое число $$$t$$$ ($$$1 \le t \le 10^5$$$) — количество наборов входных данных. Далее следует описание наборов входных данных.
Первая строка каждого набора входных данных содержит число $$$n$$$ ($$$1 \le n \le 2 \cdot 10^5$$$) — количество вершин в дереве.
Следующие $$$n-1$$$ строк каждого набора входных данных содержат по два числа — $$$u$$$, $$$v$$$, задающие ребро между $$$u$$$ и $$$v$$$ ($$$1 \le u, v \le n$$$).
Гарантируется, что сумма значений $$$n$$$ по всем наборам входных данных не превосходит $$$2 \cdot 10^5$$$.
Для каждого набора входных данных выведите сумму по модулю $$$10^9+7$$$.
161 21 33 43 53 6
288
Найдём $$$F(A)$$$ для расстановки $$$A = [0,1,0,0,1,1]$$$ ($$$A[i]$$$ означает значение вершины $$$i$$$). Состояние дерева в момент времени $$$t = 0$$$ изображено ниже. В каждой вершине записаны два числа: ее номер, затем ее значение. $$$S(0)$$$ в такой конфигурации равно $$$3$$$.
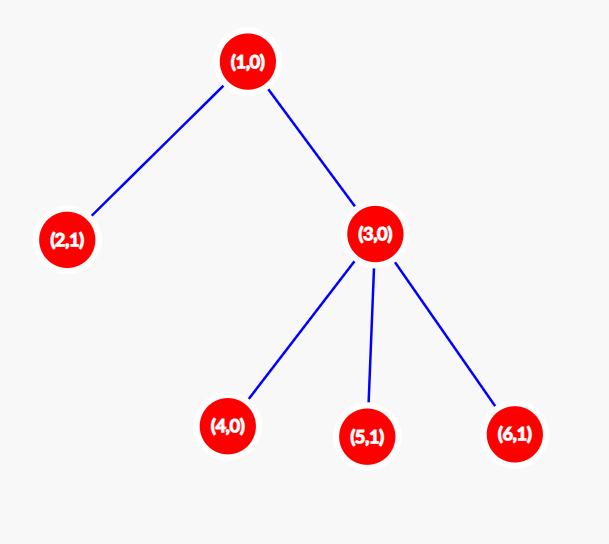
В момент $$$t = 1$$$ конфигурация меняется на $$$[1,0,0,0,0,0]$$$. Дерево будет выглядеть так, как показано на рисунке ниже. Имеем $$$S(1) = 1$$$.
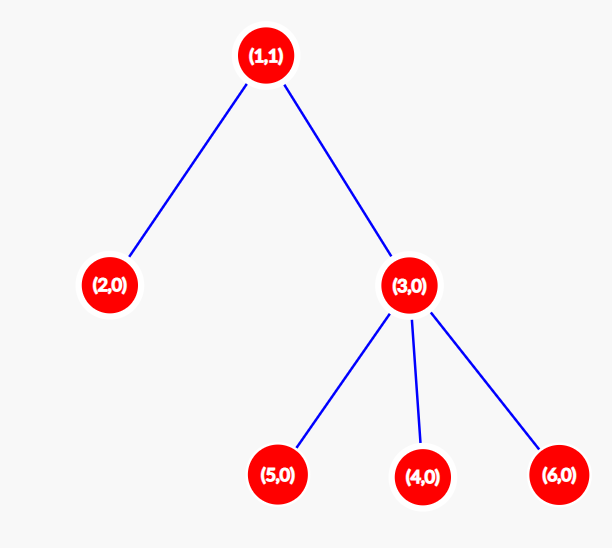
В момент $$$t = 2$$$ конфигурация меняется на $$$[0,0,0,0,0,0]$$$. Дерево будет выглядеть так, как показано на рисунке ниже. Имеем $$$S(2) = 0$$$.
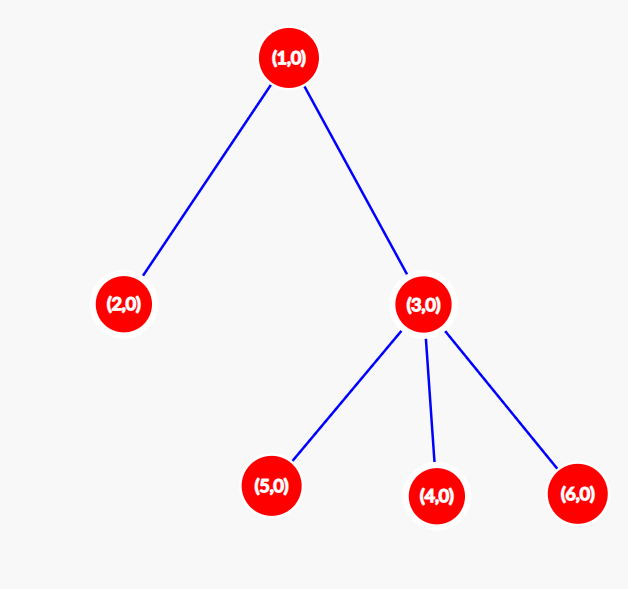
Для всех $$$t>2$$$ граф остаётся неизменным, то есть $$$S(t)=0$$$ для всех $$$t > 2$$$. Поэтому изначальная расстановка $$$A = [0,1,0,0,1,1]$$$ имеет значение $$$F(A) = 3 + 1 = 4$$$.
Выполнив аналогичный процесс для всех $$$2^{6}$$$ возможных стартовых расстановок, получим ответ $$$\textbf{288}$$$.
| Название |
|---|




